支持向量机(Support Vector Machine,SVM)

前言

好记性不如烂笔头，写下来的才是自己的。本篇博客将记录笔者学习机器学习算法——支持向量机的笔记。

优化目标

在监督学习中，许多学习的性能都非常类似，因此，重要的不是你该选择学习算法 A 还是学习算法 B，而是依赖于设计者的设计水平：比如为算法进行的特征量的选择，以及如何选择正则化参数。支持向量机是一个广泛应用于工业界和学术界的机器学习算法，与逻辑回归和神经网络相比，SVM 在学习复杂的非线性方程的时候提供了一种更为清晰强大的方式。

为了描述 SVM ，本文将从优化目标开始，然后以逻辑回归为切入点，开始展示如何通过一步步的修改来得到本质上的 SVM。

回顾以下，在逻辑回归中，我们有如下结论：

如果 $y=1$，那么 $h_θ(x) \approx 1$ 即 $θ^{T} x \gg 0$
如果 $y=0$，那么 $h_θ(x) \approx 0$ 即 $θ^{T} x \ll 0$

其中 $h_θ(x) = \frac{1}{1+e^{-\theta ^{T}x}}$

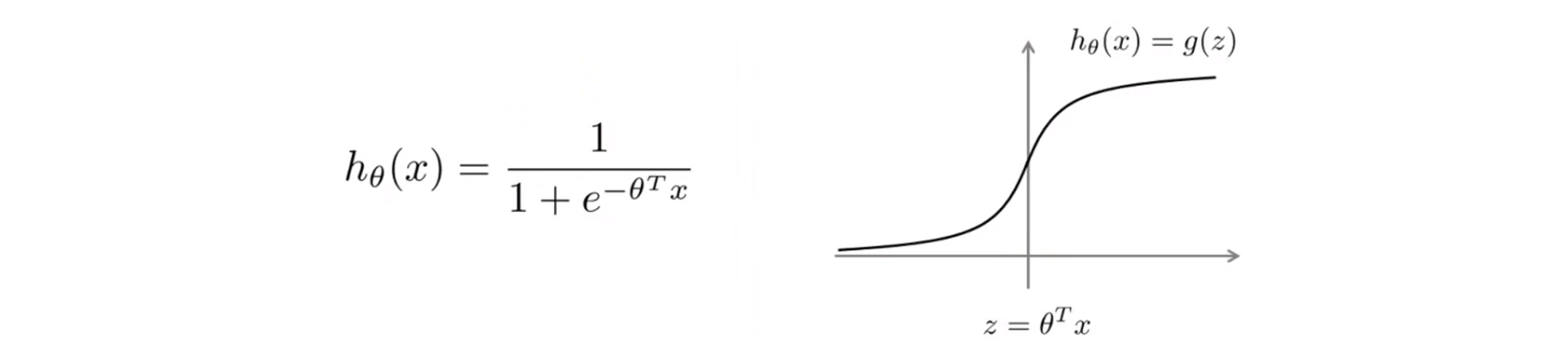
如果有一个 $y=1$ 的样本，现在我们希望 $h_θ(x)$ 趋近 $1$，这就意味着当 $h_θ(x)$ 近于 $1$ 时， $θ^{T}$ 应当远大于 $0$，由于 $z$ 表示 $θ^{T}x$ ，即到了该图的右边，不难发现此时逻辑回归的输出将趋近于 $1$。相反地，如果我们有另一个样本，即 $y=0$。我们希望假设函数的输出值将趋近于 0，这对应于 $θ^{T}x$，或者就是 $z$ 会远小于 $0$。

进一步，我们来回顾一下逻辑回归的代价函数：

$\begin{align} J(\theta ) &= \frac{1}{m} \sum_{i=1}^{m} \left [ - y^{(i)} log \left (h_\theta (x^{(i)})\right)- \left (1-y^{(i)} \right )log \left (1-h_\theta (x^{(i)}) \right )\right ]\\ &= \frac{1}{m} \sum_{i=1}^{m} \left [ - y^{(i)} log \left (\frac{1}{1+e^{-\theta ^{T}x^{(i)}}}\right )- \left (1-y^{(i)}\right )log \left (1-\frac{1}{1+e^{-\theta ^{T}x^{(i)}}} \right )\right ] \end{align}$

为了方便讨论我们将 $\theta ^{T}x^{(i)}$ 用 $z$ 代替，现在，一起来考虑两种情况：一种是 $y=1$ 的情况；另一种是 $y=0$ 的情况。

在第一种情况中，假设 $y=1$ ，此时的目标函数（代价函数）只有第一项起作用，我们得到：

$- log \left (\frac{1}{1+e^{-z}}\right )$

在第二种情况中，假设 $y=0$ ，此时的目标函数（代价函数）只有第二项起作用，我们得到：

$- log \left (1-\frac{1}{1+e^{-z}}\right )$

为了分析代价函数的趋势，得出其优化解，我们把这两项关于 $z$ 即 $θ^{T}x$ 的函数图像画出来，得到两条光滑的 sigmoid 函数曲线。

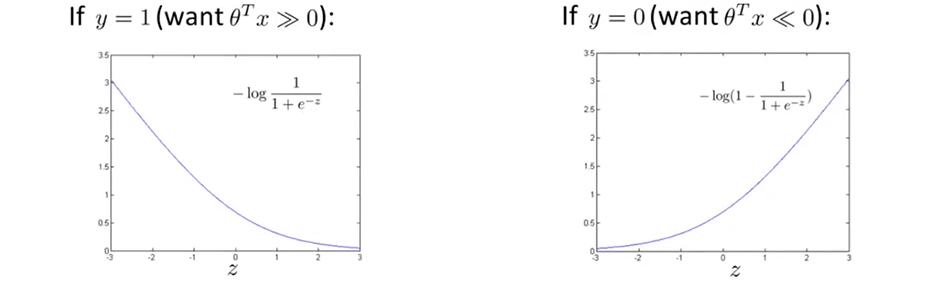
进一步地，使用两段直线来尝试替代曲线，这被称作 hinge loss 函数。

可以看到，使用替代的 hinge loss 函数后，当 $θ^{T}x$ 比 $1$ 大的时候，我们有第一项为 $0$ ；当 $θ^{T}x$ 比 $-1$ 小的时候，我们有第二项为 $0$ 。

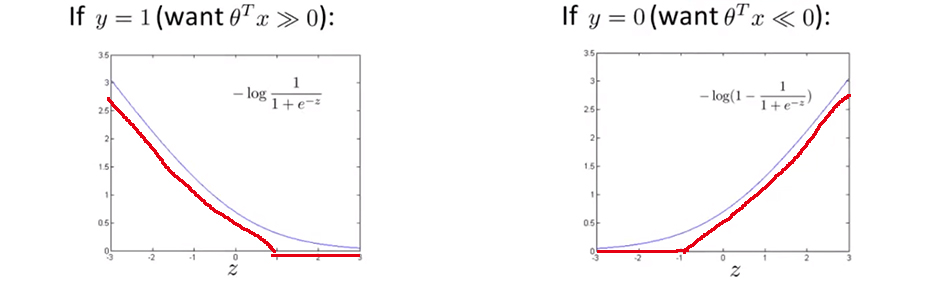
现在开始建立支持向量机，从上边的这个代价函数开始，也就是将 $- log \left (\frac{1}{1+e^{-z}}\right )$ 这一项定义为 $cost_1(z)$，将$-log \left (1-\frac{1}{1+e^{-z}}\right )$ 这一项定义为 $cost_0(z)$，那么可以得到它们的取值范围如下：

$z = θ^Tx$ $cost_1(z) = max(0,k(1-z))$ $cost_0(z) = max(0,k(1+z))$

其中 $k$ 是替代直线的斜率。

接下来，我们引入正则项。首先逻辑回归的正则化代价函数为：

$J(\theta ) = \frac{1}{m} \sum_{i=1}^{m} \left [ - y^{(i)} log \left (h_\theta (x^{(i)})\right)- \left (1-y^{(i)} \right )log \left (1-h_\theta (x^{(i)}) \right )\right ] + \frac{\lambda }{2m}\sum_{j=1}^{n} \theta _j^2$

接着我们如前所述，用 $cost_0(z)$和 $cost_1(z)$ 来替代第一项和第二项：

$J(\theta ) = \frac{1}{m} \sum_{i=1}^{m} \left [ y^{(i)} cost_1 \left (θ^T x^{(i)}\right) + \left (1-y^{(i)} \right )cost_0 \left (θ^T x^{(i)}\right)\right ] + \frac{\lambda }{2m}\sum_{j=1}^{n} \theta _j^2$

接着我们稍加变形，乘上一个$\frac{m}{λ}$，那么 SVM 的代价函数化为：

$J(\theta ) = \frac{1}{λ} \sum_{i=1}^{m} \left [ y^{(i)} cost_1 \left (θ^T x^{(i)}\right) + \left (1-y^{(i)} \right )cost_0 \left (θ^T x^{(i)}\right)\right ] + \frac{1 }{2}\sum_{j=1}^{n} \theta _j^2$

我们记 $C = \frac{1}{λ}$，那么有：

$J(\theta ) =C \sum_{i=1}^{m} \left [ y^{(i)} cost_1 \left (θ^T x^{(i)}\right) + \left (1-y^{(i)} \right )cost_0 \left (θ^T x^{(i)}\right)\right ] + \frac{1 }{2}\sum_{j=1}^{n} \theta _j^2$

这就是通常使用的 SVM 代价函数，这个系数 $C$ 本质上和 $λ$ 一样的，都是改变普通代价函数项和正则项的权重关系。也就是说，如果我们想要加强正则化强度来处理过拟合，那么减小 $C$ ；如果想要减少正则化强度来处理欠拟合，那么增大 $C$。

最后有别于逻辑回归输出的概率。在这里，我们当最小化代价函数参数 $θ$ 时，支持向量机所做的是用它来直接预测 $y$ 的值等于 $1$还是等于 $0$。因此，当 $θ^{T}x$ 大于或者等于 $0$ 时，这个假设函数会预测 $1$。

$h_\theta (x) = \left\{\begin{matrix} 1 & if\ \ \theta ^Tx\geqslant 0\\ 0 & otherwise \end{matrix}\right.$

大间距分离器

SVM 有时被称作大间距分离器(Large Margine Classification)，其原因在于 SVM 的模拟函数在使输出为 $1$ 或者 $0$ 中间增加了一个安全距离（决策边界），现在的需求是不仅仅要能正确分开输入的样本，即不仅仅要求 $θ^Tx>0$ ，这就相当于在支持向量机中嵌入了一个额外的安全因子，或者说安全的间距因子。

首先我们回顾一下上一节的结论，由于引入了 hinge loss 函数来代替 sigmoid 函数，其输出关系如下：

如果想要预测 $y=1$，那么我们需要使 $θ^Tx\geqslant 1$ （注意不仅仅是 $\geqslant 0$ ）
如果想要预测 $y=0$，那么我们需要使 $θ^Tx\leqslant −1$（注意不仅仅是 $ < 0$ ）

假如代价函数中我们使用了一个比较大的 $C$，例如 $C = 10000$。基于上面的结论，如果我们需要使得代价函数较小的话，那么需要令 $\sum_{i=1}^{m} \left [ y^{(i)} cost_1 \left (θ^T x^{(i)}\right) + \left (1-y^{(i)} \right )cost_0 \left (θ^T x^{(i)}\right)\right ] \to 0$，才能让整个代价函数的值变得很小。

此时代价函数的结果可近似为：

$\begin{align} J(\theta ) &= C \cdot 0 + \frac{1 }{2}\sum_{j=1}^{n} \theta _j^2\\ &= \frac{1 }{2}\sum_{j=1}^{n} \theta _j^2 \end{align}$

在SVM算法中，决策边界的性质是：尽可能地远离正数据集与负数据集。为什么这样做呢？因为这样会使决策边界对于两种数据集都有一些余地，也就是有一些容错率。至于其数学原理，后边再讨论。

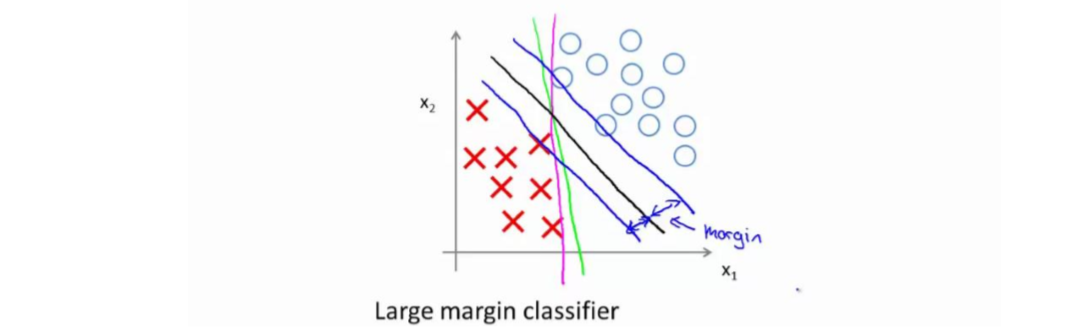
具体而言，如果你考察这样一个数据集，其中有正样本，也有负样本，可以看到这个数据集是线性可分的。即，存在一条直线把正负样本分开。当然有多条不同的直线，可以把正样本和负样本完全分开，如下图，虽然三条线都能够将样本分开，但是很明显，黑色的线要好于另外两条。直观上说，黑线看起来是更稳健的决策界。在分离正样本和负样本上它显得的更好。数学上来讲，这是什么意思呢？这条黑线有更大的距离，这个距离叫做间距(Margin)。

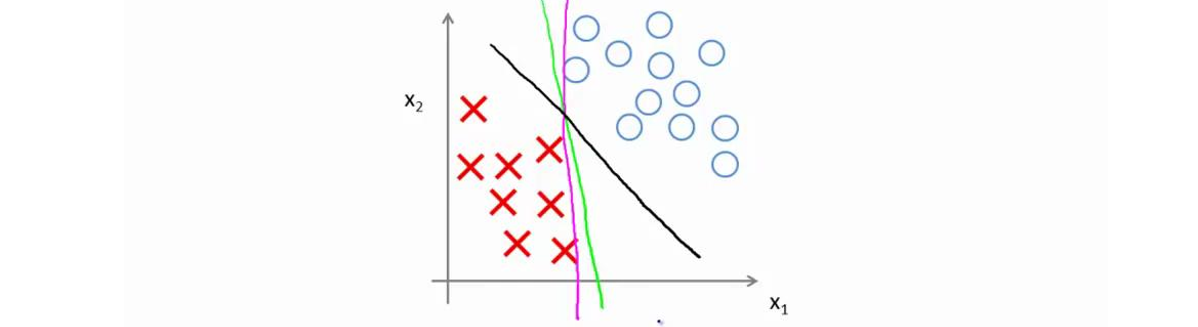
因此，下图中画出的这两条额外的蓝线之间的这个距离叫做支持向量机的间距，而这是支持向量机具有鲁棒性的原因，因为它努力用一个最大间距来分离样本。因此支持向量机有时被称为大间距分类器，而这其实是求解上一节优化问题的结果。

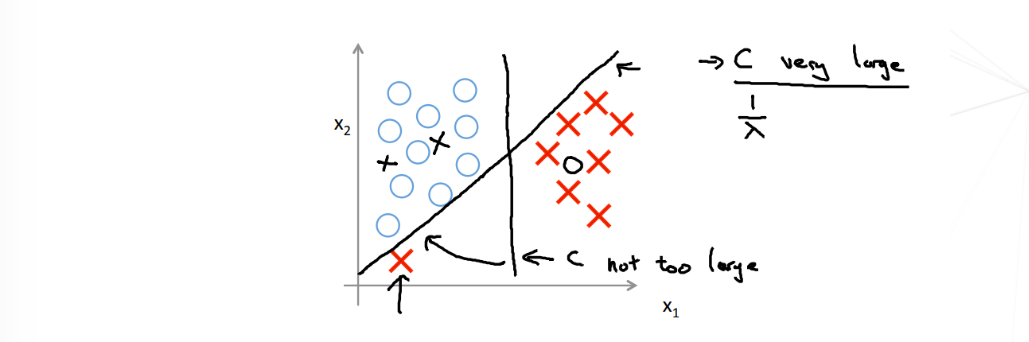
当我们选择了非常大的 $C$ 之后，对于学习算法而言，会产生过拟合的效果，如下图，在左下角有一个红叉样本，如果 $C$ 很大，决策边接就会去拟合这个样本，结果就会出现由原来竖的边界变为斜着的，但直观上我们就知道，这种改变是很糟糕的。因此，大间距分类器的描述，仅仅是从直观上给出了正则化参数 $C$ 非常大的情形，但是实际上应用支持向量机的时候，当 $C$ 不是非常非常大的时候，它可以忽略掉一些异常点的影响，得到更好的决策界。甚至当你的数据不是线性可分的时候，支持向量机也可以给出好的结果。

回顾 $C=\frac{1}{λ}$，因此：

$C$ 较大时，相当于 $λ$ 较小，可能会导致过拟合，高方差。
$C$ 较小时，相当于 $λ$ 较大，可能会导致低拟合，高偏差。

大间距分离器的数学解释

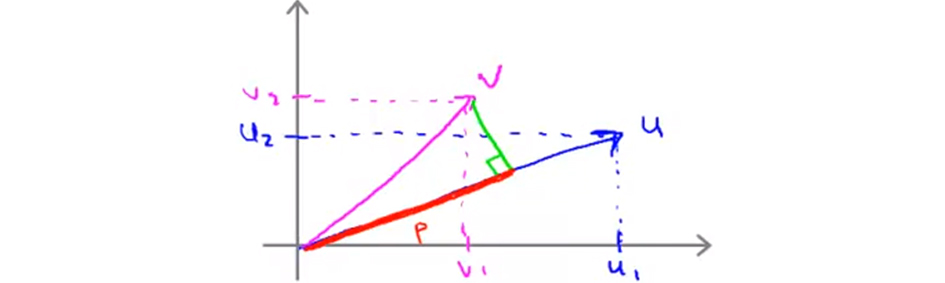
假设我们有两个向量 $u$ 和 $v$：

$u=\begin{bmatrix} u_1\\ u_2 \end{bmatrix}\ \ \ \ \ \ \ \ \ \ \ \ v=\begin{bmatrix} v_1\\ v_2 \end{bmatrix}$

那么向量 $v$ 的长度 $\sqrt{v_1^2+v_2^2}$ 就记作 $||v||$ ，$v$ 到 $u$ 的投影就记作 $p$，上图的红色线段就代表 $p$ ，那么有：

$p = ||v||cosθ$ $u^Tv = p \cdot ||u||$ $u^Tv = ||v|| \cdot ||u||cosθ$

如果将 $u$ 和 $v$ 各自单独分出两个分向量，那么有：

$u^Tv = v^Tu = p \cdot ||u|| = u_1v_1+u_2v_2$

最后一点，需要注意的就是 $p$ 值，$p$事实上是有符号的，即它可能是正值，也可能是负值，在内积计算中，如果 $u$和 $v$ 之间的夹角小于 90 度，那么那条红线的长度 $p$ 就是正值。然而如果这个夹角大于 90 度，则 $p$ 将会是负的。

我们使用这些关于向量内积的性质试图来理解支持向量机中的目标函数。

$\begin{align} &\underset{θ}{min}\frac{1}{2}\sum_{j=1}^{n}θ_j^2 \\ & s.t.\ \ \ θ^Tx^{(i)} \geqslant 1 \ \ \ \ \ \ \ \ \ \ if\ \ y^{(i)} = 1 \\ & \ \ \ \ \ \ \ \ \ \ θ^Tx^{(i)} \leqslant -1 \ \ \ \ \ \ \ if\ \ y^{(i)} = 0 \\ \end{align}$

由上面的投影观点，对于正则项我们可以得出：

$\begin{align} &\underset{θ}{min}\frac{1}{2}\sum_{j=1}^{n}θ_j^2 \\ &= \frac{1}{2}\left ( θ_1^2 + θ_2^2 +θ_3^2 +\ \ ...\ \ +θ_n^2 \right ) \\ &= \frac{1}{2} \left ( \sqrt{θ_1^2 + θ_2^2 +θ_3^2 +\ \ ... \ \ +θ_n^2}\right )^2 \\ &=\frac{1}{2}||θ||^2 \end{align}$

因此支持向量机做的全部事情，就是极小化参数向量 $θ$ 范数的平方，或者说长度的平方。

如下图所示，红叉代表样本点，蓝线是特征参数向量 $θ$，则 $x^{(i)}$ 在特征向量 $θ$ 上的投影就是 $p^{(i)}$ 红色那根线段。

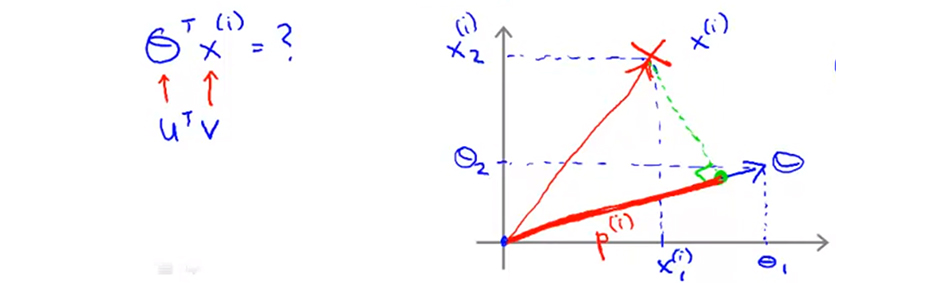
所以对于 $θ^Tx^{(i)}$ 我们可以将其理解为向量 $x$ 在向量 $θ$ 上的投影：

$θ^Tx^{(i)} = θ_1x_1^{(i)}+θ_2x_2^{(i)}+θ_3x_3^{(i)}+ \ \ ...\ \ +θ_nx_n^{(i)} = p^{(i)} \cdot ||θ||$

因为 $θ^Tx^{(i)} = p^{(i)} \cdot ||θ||$ ，将其写入我们的优化目标，$θ^Tx^{(i)}$ 也就变成了 $p^{(i)} \cdot ||θ||$ 。

这个时候我们的优化目标（目标函数）变成了：

$\begin{align} &\underset{θ}{min}\frac{1}{2}\sum_{j=1}^{n}θ_j^2 \\ & s.t.\ \ \ p^{(i)} \cdot ||θ|| \geqslant 1 \ \ \ \ \ \ \ \ \ \ if\ \ y^{(i)} = 1 \\ & \ \ \ \ \ \ \ \ \ \ p^{(i)} \cdot ||θ|| \leqslant -1 \ \ \ \ \ \ \ if\ \ y^{(i)} = 0 \\ \end{align}$

我们通过两个例子来具象的去理解上边的优化目标函数：

第一个例子：

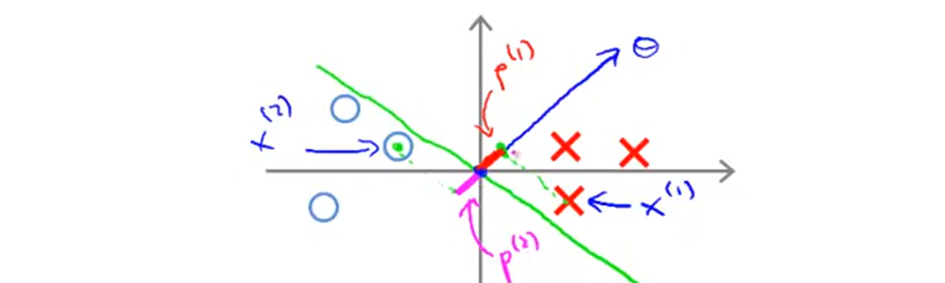
绿色的是决策边界，则特征向量和决策边界正交，也就是蓝色箭头方向。这个时候，样本点在特征向量的投影长度 $p^{(i)}$ 都会是非常小的数。如图所示：

对于正样本 $x^{(1)}$ 而言，我们需要满足条件 $p^{(1)} \cdot ||θ|| \geqslant 1$ ，但是我们发现这种边界情况下的投影，也就是图中的 $p^{(1)}$ 非常小，就会使得为了满足不等式条件而让 $θ$ 的范数足够大；
同样的对于假样本 $x^{(2)}$ 而言，我们需要满足条件 $p^{(2)} \cdot ||θ|| \leqslant -1$ ，但是我们发现这种边界情况下的投影，也就是图中的 $p^{(2)}$ 也非常小，同样的为了满足不等式条件， $θ$ 的范数也足够大才行。

但是我们的目标是：$\underset{θ}{min}\frac{1}{2}\sum_{j=1}^{n}θ_j^2$，是要最小化 $θ$，因此，上边例子看起来不是一个好的参数选择方案。

我们再来看另一个例子：

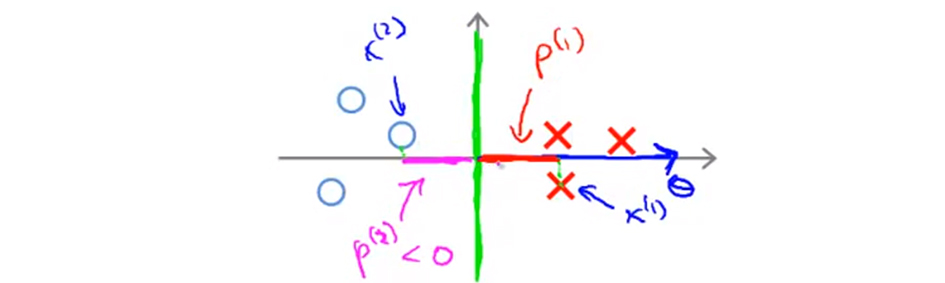
垂直线是决策界（绿色），则特征向量和决策边界正交，也就是蓝色箭头方向。这个时候同样和上边那个例子一样，取一个正例 $x^{(1)}$，一个反例 $x^{(2)}$ 这个时候你发现他们的投影长度 $p^{(1)}$ 和 $p^{(2)}$ 都比第一个例子长的多，这个情况下，为了满足不等式的要求，则 $θ$ 的范式就可以小得多，这和我们需要优化的目标是一致的。

以上就是为什么支持向量机最终会找到大间距分类器的原因。因为它试图取极大化这些 $p^{(i)}$ 好在满足不等式条件下去极小化 $θ$。

最后一点，我们的推导自始至终使用了这个简化假设，就是参数 $θ_0 =0$ 。$θ_0 =0$ 的意思是我们让决策界通过原点。

核函数(Kernels)

核函数（Kernel Function）和 SVM 没有必然关系，不过是因为核函数在 SVM 算法中表现很好因此两个方法常常一起用。

之前，我们在处理非线性决策边界时，使用的方法是引入多项式

$h_θ(x) = θ_0+θ_1x_1+θ_2x_2+ θ_3x_1x_2+θ_4x_1^2+θ_5x_2^2\ ...$

我们可以用一系列的新的特征 $f$ 来替换模型中的每一项：

$h_θ(x) = θ_0+θ_1f_1+θ_2f_2+ θ_3f_3+\ ...$

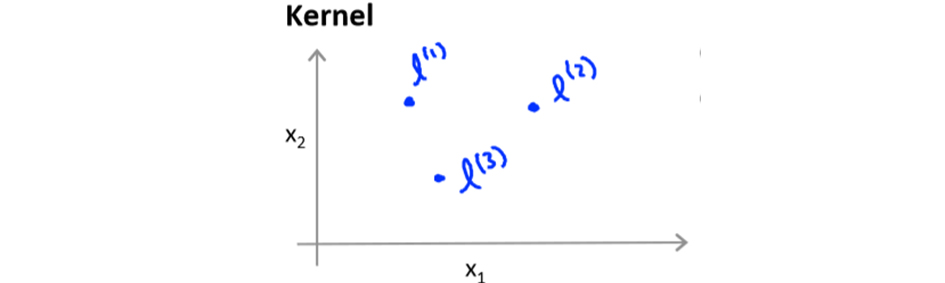
给定一个训练实例 $x$，我们利用 $x$ 的各个特征与我们预先选定的地标(landmarks) $l^{(1)}$、$l^{(2)}$、$l^{(3)}$ 的近似程度来选取新的特征 $f_1$、$f_2$、$f_3$。

为了计算数据样本 $x$ 与地标之间的接近程度，这里引入了一个新的函数 $similarity$：

$\begin{align} f_i = similarity(x,l^{(i)}) &= \exp(-\frac{||x-l^{(i)}||^2}{2\sigma^2 }) \\ &= \exp(-\frac{\sum_{j=1}^{n} \left ( x_j-l_j^{(i)} \right )^2}{2\sigma^2 }) \end{align}$

其中： $\sum_{j=1}^{n} \left ( x_j-l_j^{(i)} \right )^2$ 为样本 $x$ 的所有特征和第 $i$ 个地标 $l_j^{(i)}$ 之间的距离的和，具体形式而言，上边显示的是一个高斯核函数。

假设我们的训练实例含有两个特征 $[x_1,x_2]$，给定地标 $l^{(1)}$与不同的 $σ$ 值，见下图：

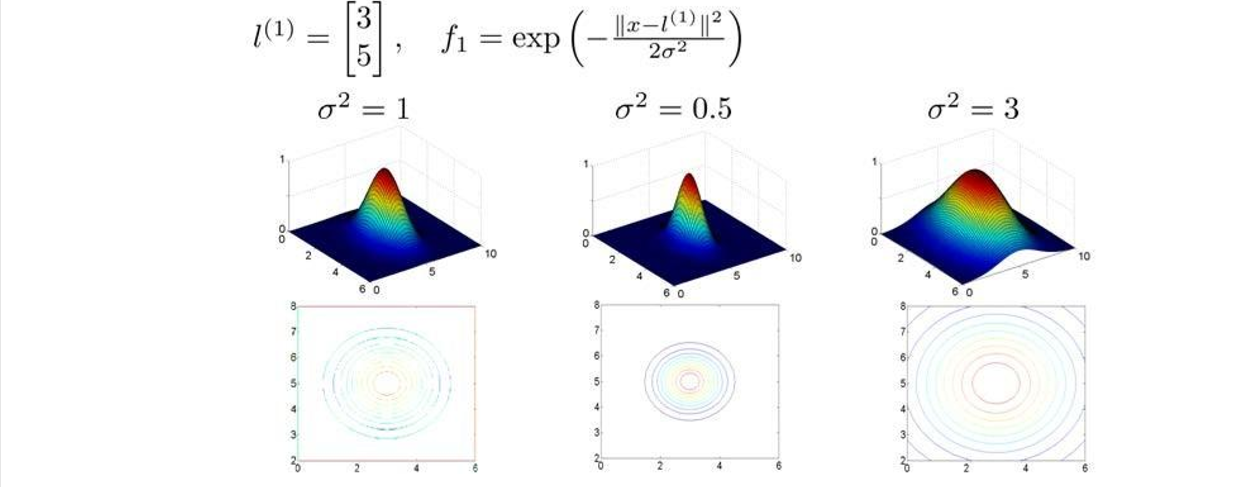
图中水平面的坐标为 $x_1$ $x_2$ ，而垂直坐标轴代表 $f$。可以看出，只有当 $x$ 与 $l^{(1)}$ 重合时 $f$ 才具有最大值。随着 $x$ 的改变 $f$ 值改变的速率受到 $σ^2$ 的控制。

函数中有两条比较重要的性质：

如果 $x \approx l^{(i)}$，即 $x$ 离 $l^{(i)}$ 很近，那么就有 $f_i = \exp(-\frac{\approx 0^2}{2 \sigma^2})\approx 1$；
如果 $x$ 远离 $l^{(i)}$ 很近，那么就有 $f_i = \exp(-\frac{large\ number}{2 \sigma^2})\approx 0$；

如果我们有很多的地标，那么它们就可以为假设函数提供很多特征量：

$l^{(1)}\ \ \ \ \rightarrow \ \ \ \ f_1$ $l^{(2)}\ \ \ \ \rightarrow \ \ \ \ f_2$ $l^{(3)}\ \ \ \ \rightarrow \ \ \ \ f_3$ $......$

应用核函数

获取地标的一种方法是，将它们放在与训练样例完全相同的位置，也就是令： $l^{(1)}=x^{(1)},l^{(2)}=x^{(2)},l^{(3)}=x^{(3)},\ …\ ,l^{(m)}=x^{(m)}$ 这样我们可以得到 $m$ 个地标，每个地标对应着一个训练样例。

$f_1 = similarity(x,l^{(1)}),\ \ \ \ f_2 = similarity(x,l^{(2)}),\ \ \ \ f_3 = similarity(x,l^{(3)}),...$

这样做的好处在于我们得到的新特征是建立在原有特征和训练集中所有其他特征之间距离的基础之上的，即：

$f^{(i)} = \begin{bmatrix} f_0^{(i)}=1\\ f_1^{(i)}=sim(x^{(i)},l^{(1)})\\ f_2^{(i)}=sim(x^{(i)},l^{(2)})\\ \vdots \\ f_i^{(i)}=sim(x^{(i)},l^{(i)})=e^0=1\\ \vdots \\ f_m^{(i)}=sim(x^{(i)},l^{(m)}) \end{bmatrix}$

下面我们将核函数运用到支持向量机中，修改我们的支持向量机假设为：

给定 $x$ ，计算新的特侦 $f$ ，当 $θ^Tf \geqslant 0$ 时，预测 $y=1$ ，否则反之。

则修改代价函数为：

$\underset{θ}{min} \ J(\theta ) =C \sum_{i=1}^{m} \left [ y^{(i)} cost_1 \left (θ^T f^{(i)}\right) + \left (1-y^{(i)} \right )cost_0 \left (θ^T f^{(i)}\right)\right ] + \frac{1 }{2}\sum_{j=1}^{n=m} \theta _j^2$

在具体实施过程中，我们还需要对最后的正则化项进行些微调整，在计算 $\frac{1 }{2}\sum_{j=1}^{n=m} \theta _j^2 = θ^Tθ$ 时，我们用 $θ^TMθ$ 代替 $θ^Tθ$ ，其中 $M$ 是根据我们选择的核函数而不同的一个矩阵。这样做的原因是为了简化计算。

对于最小化 SVM 的代价函数的方法，通常使用现有的软件包（如 liblinear，libsvm 等）。另外，支持向量机也可以不使用核函数，不使用核函数又称为线性核函数（linear kernel）。当我们不采用非常复杂的函数，或者我们的训练集特征非常多而实例非常少的时候，可以采用这种不带核函数的支持向量机。

SVM 参数选择

这里有一些对于参数 $C$的总结：

如果 $C$ 比较大，那么我们会有更高的方差、更低的偏差（过拟合）；
如果 $C$ 比较小，那么我们会有更高的偏差、更低的方差（欠拟合）。

还有一些对于参数 $σ^2$ 的总结：

如果 $σ^2$ 比较大，那么特征量变化会更加平滑，这意味着更高的偏差、更低的方差（欠拟合）
如果 $σ^2$ 比较小，那么特征量变化会没那么平滑，这意味着更高的方差、更低的偏差（过拟合）

应用 SVM

在高斯核函数之外我们还有其他一些选择，如：

多项式核函数（Polynomial Kernel）
字符串核函数（String kernel）
卡方核函数（ chi-square kernel）
直方图交集核函数（histogram intersection kernel）
等等…

这些核函数的目标也都是根据训练集和地标之间的距离来构建新特征，这些核函数需要满足 Mercer’s 定理，才能被支持向量机的优化软件正确处理。

虽然说优化的事情大部分都叫交付给了优化软件包，但是有些超参数的选择则还需要人工来完成，下面是普遍使用的准则：

$n$ 为特征数，$m$ 为训练样本数。

如果相较于 $m$ 而言，$n$ 要大许多，即训练集数据量不够支持我们训练一个复杂的非线性模型，我们选用逻辑回归模型或者不带核函数的支持向量机。
如果 $n$ 较小，而且 $m$ 大小中等，例如 $n$ 在 $1-1000$ 之间，而 $m$ 在 $10-10000$ 之间，使用高斯核函数的支持向量机。
如果 $n$ 较小，而 $m$ 较大，例如 $n$ 在 $1-1000$ 之间，而 $m$ 大于 $50000$，则使用支持向量机会非常慢，解决方案是创造、增加更多的特征，然后使用逻辑回归或不带核函数的支持向量机。

本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：黄钢的博客，同时保持文章内容的完整和以上声明信息！

机器学习算法阅读笔记系列——支持向量机

前言