生成对抗网络——FGAN和WGAN

前言

自从 Generative Adversarial Nets 被提出来之后，GAN就存在训练困难，梯度消失等问题。FGAN，《Training Generative Neural Samplers using Variational Divergence Minimization 》的论文阐述了关于衡量两个分布的差距不仅限于JSDivergence ，并给出了挑选合适的衡量两个分布差距的标准。WGAN的提出，提出了一个量化衡量损失的办法，该方法代表这个数值越小代表GAN训练得越好，代表生成器产生的图像质量越高。跟该技术相关的论文其实有两篇：《Towards Principled Methods for Training Generative Adversarial Networks》里面推了一堆公式定理，从理论上分析了原始GAN的问题所在，在第二篇《Wasserstein GAN》最终给出了改进的算法实现流程。有些内容来自台湾大学李宏毅老师的线上资源：李宏毅机器学习

本篇博客有大量公式演示，不推荐使用手机查看

回顾传统 GAN 算法

初始化一个由 $θ_D$ 决定的 $D$ 和由 $θ_G$ 决定的 $G$；
循环迭代训练过程：
- 训练判别器（D）的过程，循环 $k$ 次：
  - 从真实分布 $P_{data}(x)$ 中抽样 $m$个正例 $\lbrace x^{(1)},x^{(2)},x^{(3)},…,x^{(m)} \rbrace$
  - 从先验分布 $P_{prior}(x)$ 中抽样 $m$个噪声向量 $\lbrace z^{(1)},z^{(2)},z^{(3)},…,z^{(m)} \rbrace$
  - 利用生成器 $\tilde x^i = G(z^i)$ 输入噪声向量生成 $m$ 个反例 $\lbrace \tilde x^{(1)},\tilde x^{(2)},\tilde x^{(3)},…,\tilde x^{(m)} \rbrace$
  - 最大化 $\tilde V$ 更新判别器参数 $θ_D$：
    - $\tilde V = \frac{1}{m}\sum_{i=1}^{m} log D(x^i) + \frac{1}{m}\sum_{i=1}^{m} log (1-D(\tilde x^i))$
    - $θ_D := θ_D - \eta \nabla \tilde V(θ_D)$
- 训练生成器（G）的过程，循环 $1$ 次：
  - 从先验分布 $P_{prior}(x)$ 中抽样 $m$个噪声向量 $\lbrace z^{(1)},z^{(2)},z^{(3)},…,z^{(m)} \rbrace$
  - 最小化 $\tilde V$ 更新生成器参数 $θ_G$：
    - $\require{cancel}\tilde{V}=\cancel{\frac{1}{m}\sum_{i=1}^m\log D(x^i)}+\frac{1}{m}\sum_{i=1}^m\log(1-D(G(z^i)))$
    - $θ_G := θ_G - \eta \nabla \tilde V(θ_G)$

F Divergence (F-Divergence)

原始 GAN 采用的是 JS Divergence 来衡量两个分布之间的距离。除此之外这个世界上还存在着各种各样的 Divergence，例如 KL Divergence 、 Reverse KL divergence。那么这些 Divergence 之间是否具有什么“统一”的模式呢？事实上真的有这样的统一模式的存在。它就是 F-Divergence。

在这里我们先来了解一下什么是 F Divergence 。设定 $P$ 和 $Q$ 是两个不同的分布， $p(x)$ 和 $q(x)$ 代表着分别从 $P$ 和 $Q$ 采样出 $x$ 的几率，则我们将F-Divergence 定义为：

$D_f(P||Q) = \int_{x} q(x)f\left ( \frac{p(x)}{q(x)} \right )dx$

上述公式衡量和$P$ 和 $Q$有多不一样，公式里边的函数 $f$ 可以是很多不同的版本，只要 $f$ 满足以下条件：它是一个凸函数同时 $f(1) = 0$ 。

稍微分析一下这个公式：

假设对于所有的 $x$ 来说，都有 $p(x) = q(x)$，则有$D_f(P,Q) = 0$，也就是意味着两个分布没有区别，和假设一样。
同时 0 是$D_f$ 能取到的最小值：

$D_f(p||q) = \int_{x} q(x)f\left ( \frac{p(x)}{q(x)} \right )dx \geq f\left ( \int q(x)\frac{p(x)}{q(x)}dx \right ) = f(1) = 0$

也就是说，只要两个分布稍有不同，就能通过 $D_f$ 得到的正值反映出来。这个时候我们发现之前常用的 KL Divergence 其实就是 F Divergence 的一种。

当你设置 $f(x) = x\ log\ x$ ，即将 F Divergence 转换为了 KL Divergence 了。

$D_f(P||Q)=\int_x q(x)\frac{p(x)}{q(x)}\log(\frac{p(x)}{q(x)})dx=\int_xp(x)\log(\frac{p(x)}{q(x)})dx$

当你设置 $f(x) = -\ log\ x$ ，即将 F Divergence 转换为了 Reverse KL Divergence。

$D_f(P||Q)=\int_xq(x)(-\log(\frac{p(x)}{q(x)}))dx=\int_xq(x)\log(\frac{q(x)}{p(x)})dx$

当你设置 $f(x) = (x-1)^2$ ，即将 F Divergence 转换为了 Chi Square。

$D_f(P||Q)=\int_x q(x)(\frac{p(x)}{q(x)}-1)^2dx = \int_x\frac{(p(x)-q(x))^2}{q(x)}dx$

Fenchel 共轭(Fenchel Conjugate)

每一个凸函数$f(x)$他都有对应的一个共轭函数取作$f^{ * }(x)$：

$f^{* }(x) = \underset{x \in dom(f)}{max}{xt-f(x)}$

上述公式的意思就是给定 $t$ 找出一个在 $f(x)$ 里边有定义的 $x$ 使得 $xt-f(x)$ 最大，当然 $t$ 可以无限取值，那么假定我们取值 $t = t_1$ 和 $t = t_2$ 则有：

对于所有可能的变量 $t$ ，$xt-f(x)$ 对应了无数条直线：

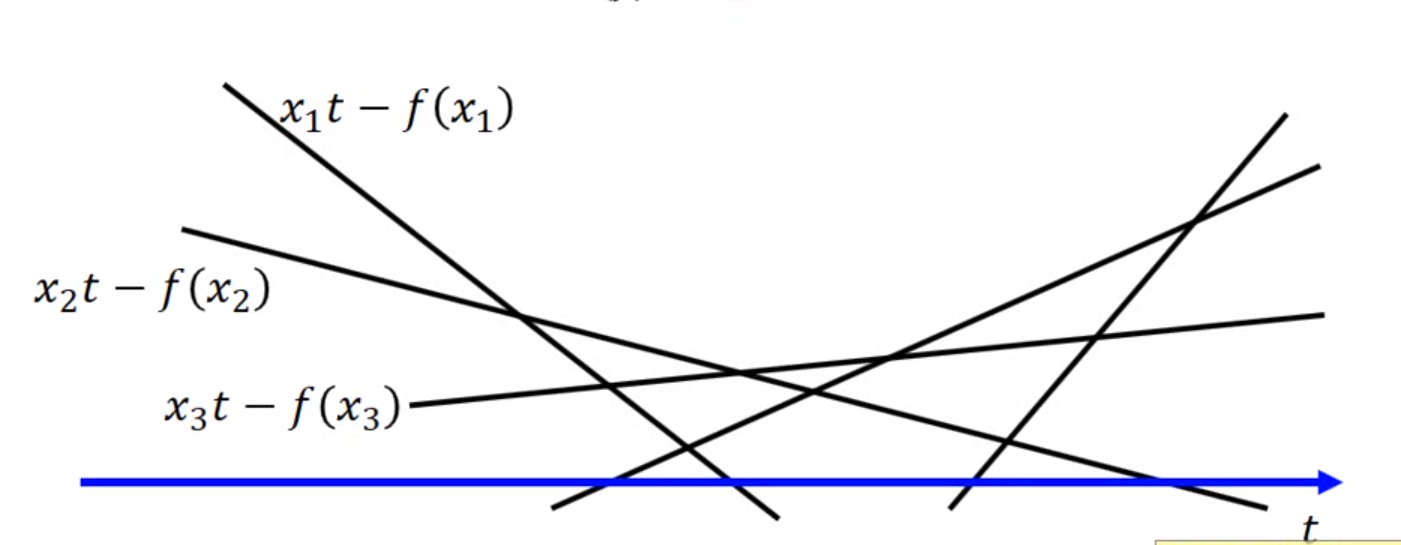
这个时候给定某个 $t$ 看看哪个 $x$ 可以取得最大值：

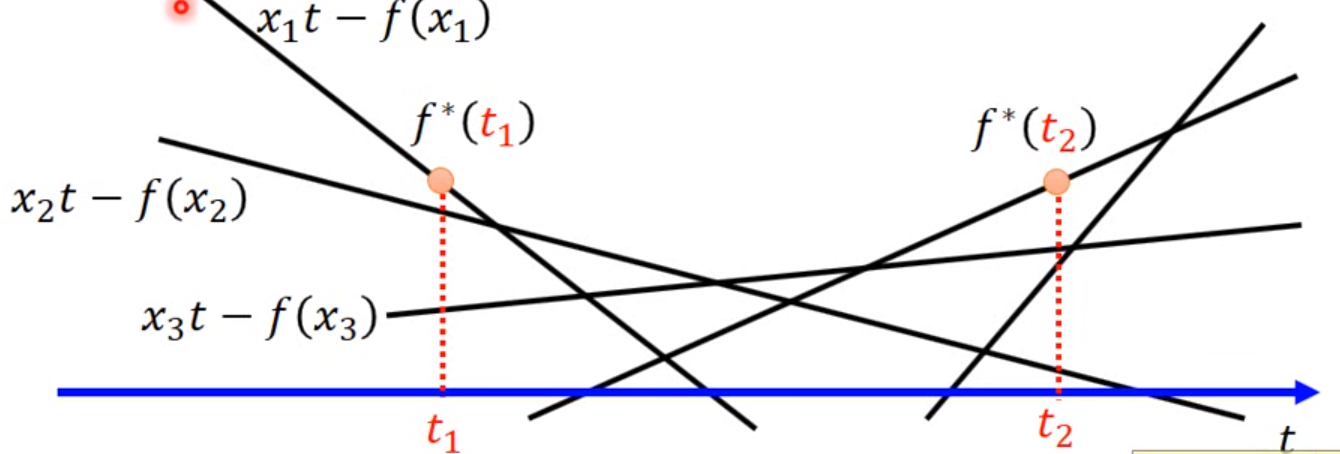
如上图，当 $t = t_1$ 的时候，找到最大点 $f^{* }(t_1)$，当 $t = t_2$ 的时候，找到最大点 $f^{* }(t_2)$，遍历所有的 $t$ 即可得到红色的这条函数就是 $f^{* }(t)$：

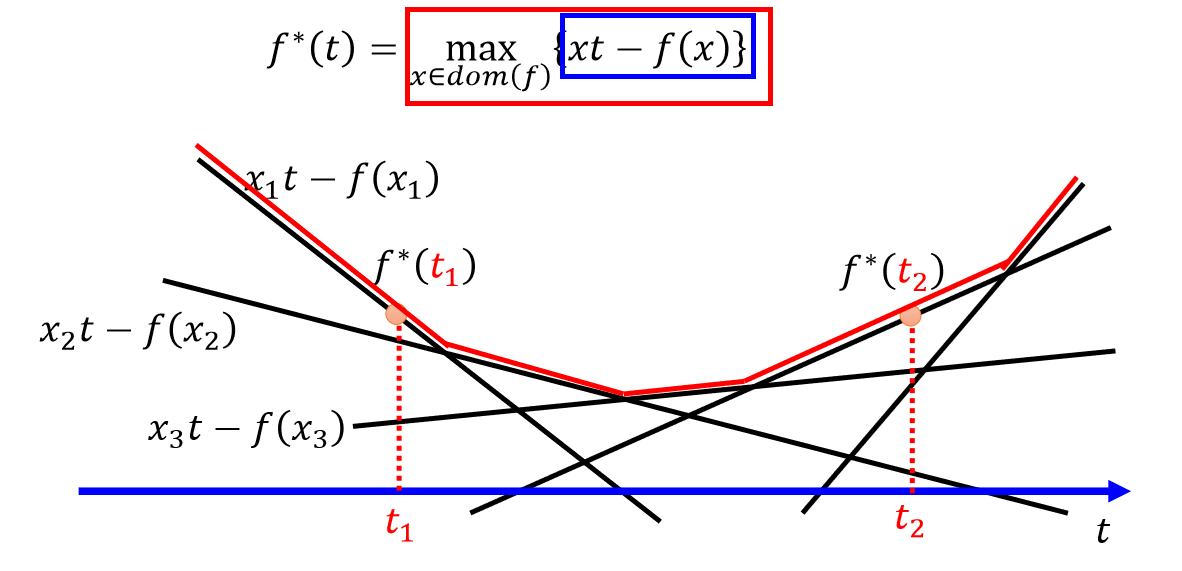
下面我们看一个具体一些的例子

当 $f(x)=x\ logx$ 时，我们可以将对应的 $f^{* }(t)$ 画出来：

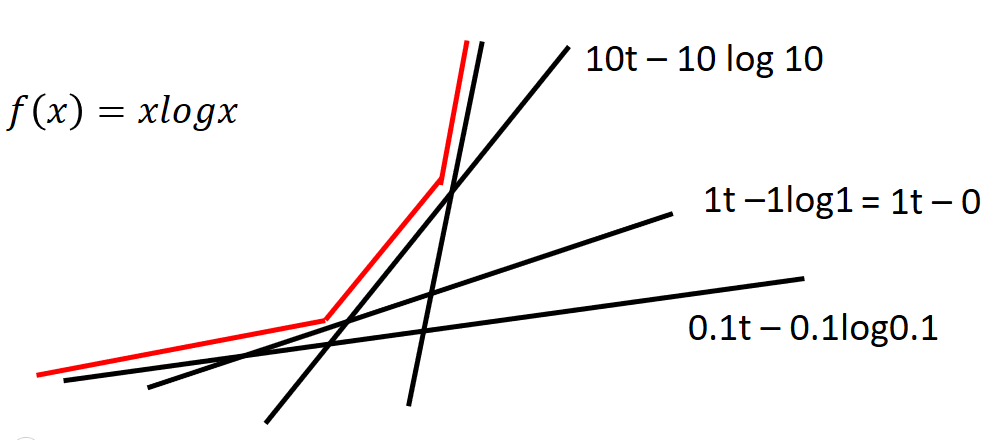
这个图实际上是一个指数函数，当 $f(x)=x\ logx$ 时，$f^{* }(t)=e^{(t−1)}$。

由于 $f^{* }(t)=\underset{x \in dom(f)}{max}{xt−f(x)}$，假设让 $g(x)=xt−x\ logx$，那么现在的问题就变成了：给定一个 $t$ 时，求 $g(x)$ 的最大值问题。对 $g(x)$ 求导并让导数为 $0$ ：$dg(x)dx=t−logx−1=0$，可解得$x=e^{(t−1)}$。再带入回原公式可得：$f^{* }(t)=e^{(t−1)}×t−e^{(t−1)}×(t−1)=e^{(t−1)}$

F-Divergence GAN

那我们怎么用上边的数学知识和 GAN 联系在一起呢？我们首先要记得这条公式，关于 $f^{* }(t)$ 和 $f(x)$ 的转换关系式：

$f^{* }(t) = \underset{x \in dom(f)}{sup}\left \{ xt-f(x) \right \} \ \ \ \ \Leftrightarrow\ \ \ \ f(x) = \underset{t \in dom(f^{* })}{max}\left \{ xt-f^{* }(t) \right \}$

利用这个关系，我们能够将 F Divergence 的定义变形为一个类似于 GAN 的式子。

$\begin{align} D_f(P||Q) & = \int_{x} q(x)f\left ( \frac{p(x)}{q(x)} \right )dx \\ & = \int_{x} q(x)\left ( \underset{t \in dom(f^{* })}{max}\left \{ \frac{p(x)}{q(x)} t-f^{* }(t) \right \} \right )dx \\ & \geqslant \int_{x} q(x)\left ( \frac{p(x)}{q(x)} D(x)-f^{* }\left (D(x)\right ) \right ) dx \\ & = \int_x p(x)D(x)dx - \int_xq(x)f^{* }(D(x))dx \\ & \approx \underset{D}{max} \int_x p(x)D(x)dx - \int_xq(x)f^{* }(D(x))dx \end{align}$

解释一下上式：

第一行就是 F Divergence 的定义式；
第三行将 $t$ 替换成 $D(x)$ 并将 $=$ 替换成 $\geqslant$ 原因是：我们要求得的是给定 $x$ 找到一个 $t$ 使得式子最大，也就是说不管 $D(x)$ 取什么值都一定小于或者等于第二行的式子；
最后一步就是，我要找到一个 $D$ 使得，式子最大，上界就是等于第二行的式子。

现在我们推导出关于 F Divergence 的变式：

$\begin{align} D_f(P||Q) & \approx \underset{D}{max} \int_x p(x)D(x)dx - \int_xq(x)f^{* }(D(x))dx \\ & = \underset{D}{max}\left \{ E_{x\sim P}\left [ D(x) \right ] - E_{x\sim Q}\left [ f^{* }(D(x) )\right ]\right \} \end{align}$

我们知道，GAN 的目的是训练生成器 G，使其产生的数据分布 $P_G$ 与真实数据的分布 $P_{data}$ 尽可能小。换言之，如果我们用 F-Divergence 来表达 $P_G$ 与 $P_{data}$ 的差异，则希望最小化
$D_f(P_{data}||P_G)$ 。

$\begin{align} D_f(P_{data}||P_G) & = \underset{D}{max}\left \{ E_{x\sim P_{data} }\left [ D(x) \right ] - E_{x\sim P_G}\left [ f^{* }(D(x) )\right ]\right \} \end{align}$

对于生成器来说，我们就是要找到一个 $P_G$ 使得有：

$\begin{align} G^{* } &= arg\ \underset{G}{min}\ D_f(P_{data} || P_G) \\ &= arg\ \underset{G}{min}\ \underset{D}{max}\left \{ E_{x\sim P_{data} }\left [ D(x) \right ] - E_{x\sim P_G}\left [ f^{* }(D(x) )\right ]\right \} \\ &= arg\ \underset{G}{min}\ \underset{D}{max}\ V(G,D) \end{align}$

上述从数学推导上给出了 $V(G,D)$ 的定义方式。但实际上要注意，此处的 $V(G,D)$ 不一定就是原生GAN的形式。 F-Divergence GAN 是对 GAN 模型的统一，对任意满足条件的 $f$ 都可以构造一个对应的 GAN。事实上，在将其应用到GAN时，有非常多的不同的生成器函数可供使用：

在这个体系下，你只需要从这个表格中挑选不同的$f^{* }(t)$就可以得到不同的 F-Divergence。而公式中的 $D(x)$，就是我们 GAN 中的判别器。

WGAN

前面我们介绍了使用 F-Divergence 来将“距离”定义到一个统一框架之中的方法。而 Fenchel Conjugate 则将这个 F-Divergence 与 GAN 联系在一起。这么做的目的在于，我们只要能找到一个符合 F-Divergence 要求的函数，就能产生一个距离的度量，从而定义一种不同的 GAN。

对于传统的 GAN 来说，选定特定的度量函数之后，会导致目标函数变成生成器分布和真实分布的 JS Divergence 度量。但是使用JS Divergence 有很多问题，比如说一个最严重的问题就是当两个分布之间完全没有重叠时，分布间距离的大小并不会直接反映在Divergence 上。这对基于迭代的优化算法是个致命问题。

基础 WGAN

Earth Mover’s Distance 用一句话描述 EM 距离：将一个分布 P 通过搬运的方式变成另一个分布 $Q$ 所需要的最少搬运代价。

比如说我们有下面的两个分布，如何将 $P$ 上的内容“匀一匀”得到 $Q$ 呢？下图展示了其中两种办法，但显然不仅仅只有这两种。既然移动的方法有很多种，如果每一种都表示了一种代价，那么显然有“好”方法，就会有“坏”方法。假设我们衡量移动方法好坏的总代价是“移动的数量”x“移动的距离”。那这两个移动的方案肯定是能分出优劣的。

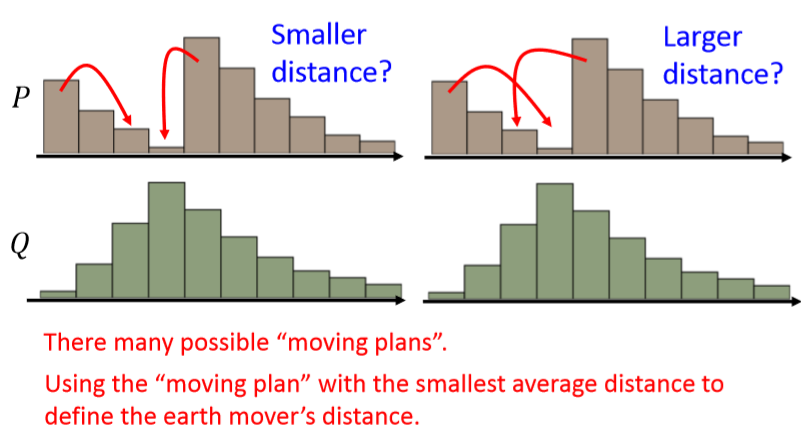
当我们用分布 $Q$ 上不同颜色的色块对应分布 $P$的相应位置，就可以将最好的移动方案画成下面这个样子：

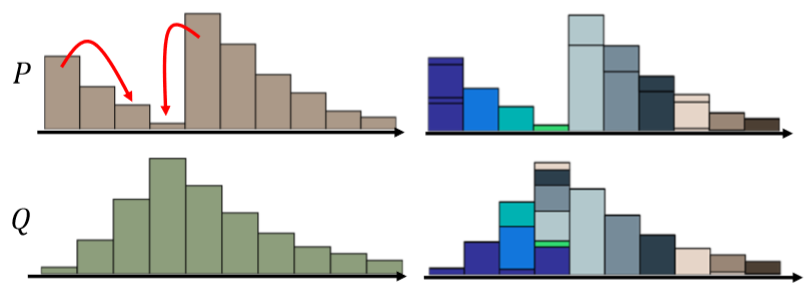
为了便于形式化定义，我们可以将这个变化画为一个矩阵：

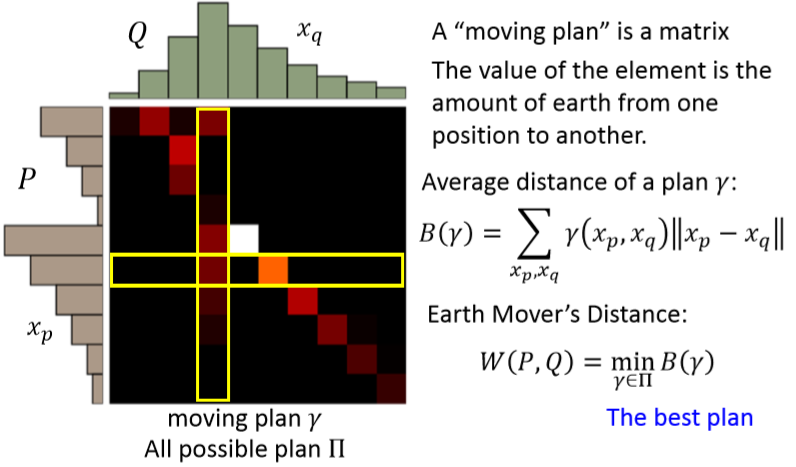
对于每一个移动方案 $\gamma$，都能有这样一个矩阵。矩阵的每一行表示分布 $P$ 的一个特定位置。该行中的每一列表示需要将该行的内容移动到分布 $Q$ 对应位置的数量。即矩阵中的一个元素$(x_p,x_q)$表示从 $P(x_p)$ 移动到 $Q(x_q)$ 的数量。

而对于方案 $\gamma$ 我们可以定义一个平均移动距离(Average distance of a plan $\gamma$)：

$B(\gamma)=\sum_{x_p,x_q}\gamma(x_p,x_q)||x_p-x_q||$

而 Earth Mover’s Distance 就是指所有方案中平均移动距离最小的那个方案：

$W(P,Q)=\min_{\gamma\in\prod}B(\gamma)$

其中 $\prod$ 是所有可能的方案。

为什么说这个 EM 距离比较好呢？因为它没有 JS Divergence 的问题。比如说，当第 $0$、$50$、$100$ 次迭代时，两个分布的样子是这样：

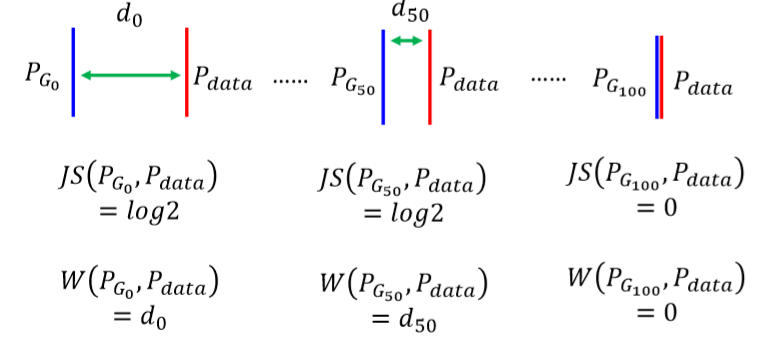
从上面的训练过程中能看出来迭代过程中 JSD 总是不变的（永远是log2），直到两个分布重叠的一瞬间，JSD 降为0 。

而当我们换成EM距离的时候，即便在两次迭代中两个分布完全没有重叠，但一定有 EM 距离上的区别。

接下来我们就将 EM 距离与 GAN 联系起来！回忆一下 F-Divergence：

$D_f(P_{data}||P_G)=\max_D\{E_{x\sim P_{data} }[D(x)]-E_{x\sim P_G}[f^{* }(D(x))]\}$

EM 距离也可以类似 F Divergence，用一个式子表示出来：

$W(P_{data},P_G)=\max_{D\in \text{1-Lipschitz} }\{E_{x\sim P_{data} }[D(x)]-E_{x\sim P_G}[D(x)]\}$

公式中 $1-Lipschitz$ 表示了一个函数集。当 $f$ 是一个 Lipschitz 函数时，它应该受到以下约束： $||f(x_1)-f(x_2)||\le K||x_1-x_2||$ 。当 $K=1$ 时，这个函数就是 $1-Lipschitz$ 函数。直观来说，就是让这个函数的变化“缓慢一些”。

图中绿色的线属于 $1-Lipschitz$ 函数，而蓝色的线肯定不是 $1-Lipschitz$ 函数。

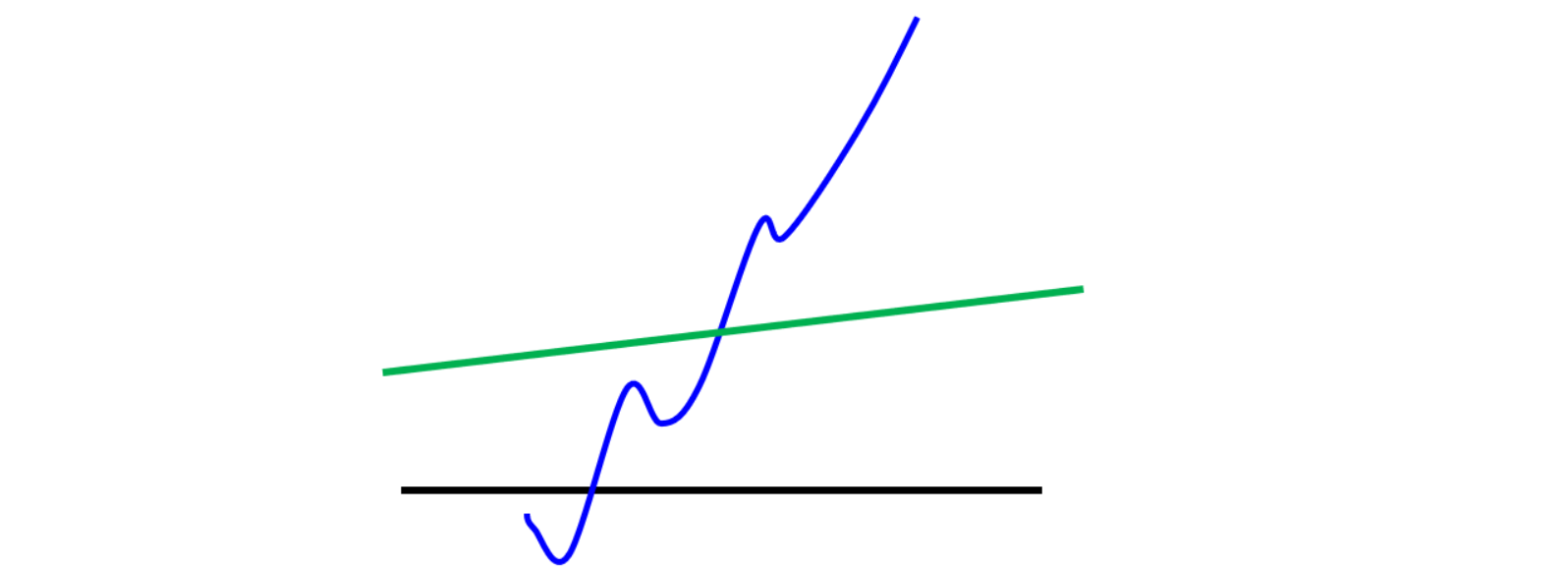
为什么要限制生成器 D 时 $1-Lipschitz$ 函数呢？我们考虑一下如果不限制它是 $1-Lipschitz$ 函数时会发生什么。

假设我们现在有两个一维的分布，$x_1$ 和 $x_2$ 的距离是 $d$，显然他们之间的 EM 距离也是 $d$ ：

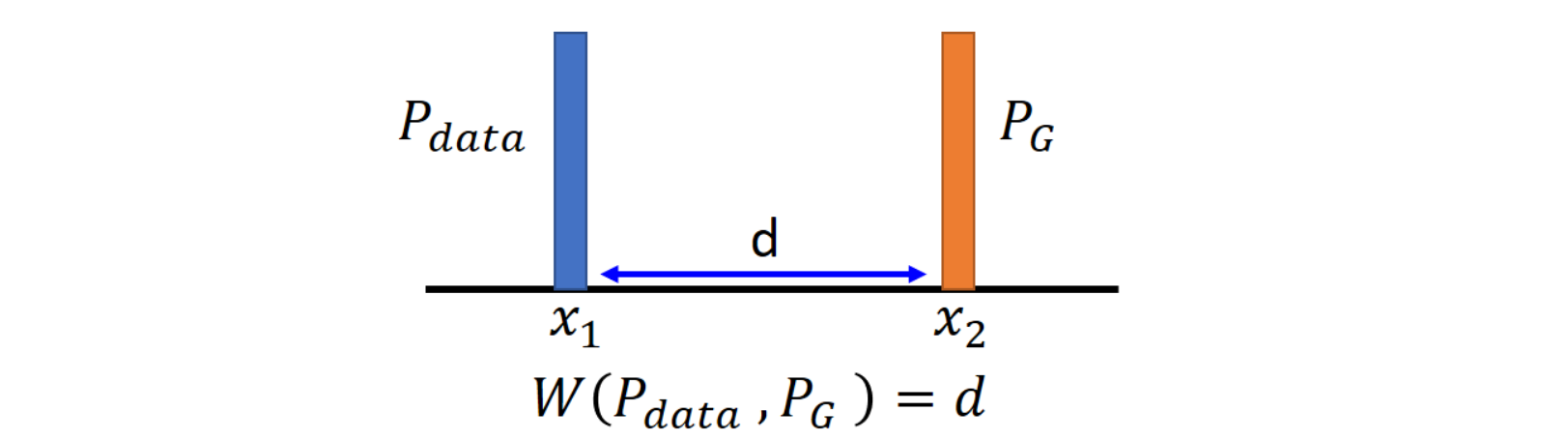
此时如果我们想要去优化 $W(P_{data},P_G)=\max_{D\in \text{1-Lipschitz} }{E_{x\sim P_{data} }[D(x)]-E_{x\sim P_G}[D(x)]}$ ，只需要让 $D(x_1)=+\infty$，而让 $D(x_2)=-\infty$ 就可以了。

也就是说，如果不加上 $1-Lipschitz$ 的限制的话，只需要让判别器判断 $P_{data}$ 时大小是正无穷，判断 $P_G$ 时是负无穷就足够了。这样的判别器可能会导致训练起来非常困难：判别器区分能力太强，很难驱使生成器提高生成分布数据质量。

这个时候我们加上了这个限制，也就是说 $||D(x_1)-D(x_2)||\le||x_1-x_2||=d$ 。此时如果我们想要满足上面的优化目标的话，就可以让 $D(x_1)=k+d$，让$D(x_2)=k$。其中 $k$ 具体是什么无所谓，关键是我们通过 $d$ 将判别器在不同分布上的结果限制在了一个较小的范围中。

这样做有什么好处呢？因为我们传统的 GAN 所使用的判别器是一个最终经过 sigmoid 输出的神经网络，它的输出曲线肯定是一个S型。在真实分布附近是 $1$ ，在生成分布附近是 $0 $。而现在我们对判别器施加了这个限制，同时不再在最后一层使用 sigmoid ，它有有可能是任何形状的线段，只要能让$D(x_1)-D(x_2)\le d$即可。如下图所示：

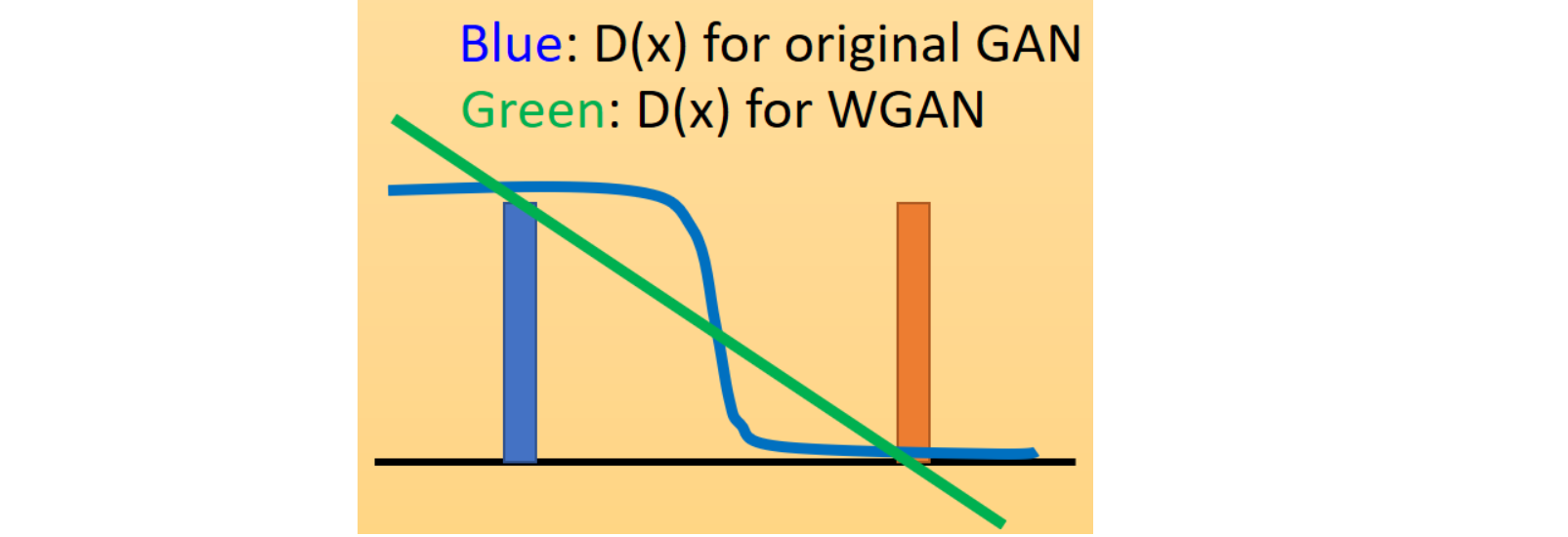
传统 GAN 的判别器是有饱和区的（靠近真实分布和生成分布的地方，函数变化平缓，梯度趋于 $0$）。而现在的 GAN 如果是一条直线，那就能在训练过程中无差别地提供一个有意义的梯度。

前面说了这么多，核心的观点就是：

不要用 sigmoid 输出。
换成受限的 $1-Lipschitz$ 来实现一个类似 sigmoid 的“范围限制”功能。

然而这个 $1-Lipschitz$ 限制应该如何施加？文章中所用的方法非常简单粗暴：截断权重。一个判别器 $D$ 的形状由其参数决定，当我们需要这个判别器满足 $1-Lipschitz$ 限制，那我们可以通过调整其参数来满足限制。

由于我们的函数是一个“缓慢变化”的函数，想要让函数缓慢变化，只需要让权值变小一些即可：

在每次参数更新之后，让每个大于 $c$ 的参数 $w$ 等于 $c$ 、让每个小于 $−c$ 的参数 $w$ 等于 $−c$，即将所有权值参数 $w$ 截断在 $[−c,c]$ 之间。然而这么做实际上保证的并不是 $1-Lipschitz$，而是 $K-Lipschitz$，甚至这个 $K$ 是多少都是玄学，只能通过调参来测试了。

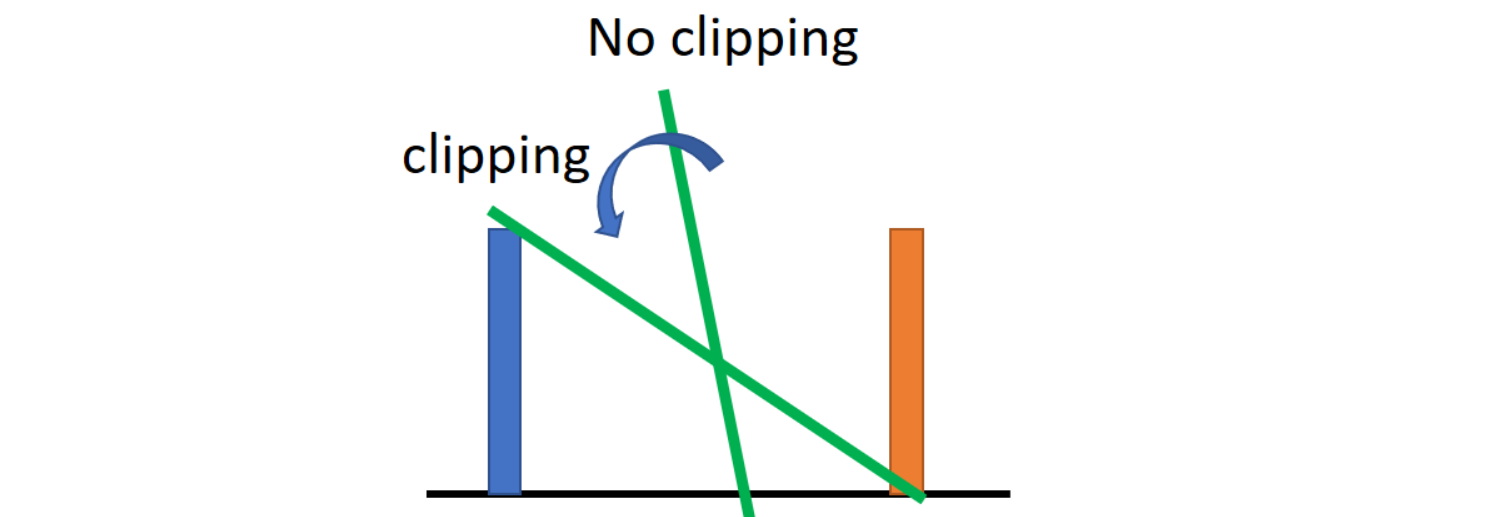
图中斜率比较陡峭的就是没有截断的函数。而截断的函数将会逆时针旋转，从而产生一个类似1-Lipschitz限制的效果。

下面我们来对原始的 GAN 算法流程做修改，先祭出原始算法：

初始化一个由 $θ_D$ 决定的 $D$ 和由 $θ_G$ 决定的 $G$；
循环迭代训练过程：
- 训练判别器（D）的过程，循环 $k$ 次：
  - 从真实分布 $P_{data}(x)$ 中抽样 $m$个正例 $\lbrace x^{(1)},x^{(2)},x^{(3)},…,x^{(m)} \rbrace$
  - 从先验分布 $P_{prior}(x)$ 中抽样 $m$个噪声向量 $\lbrace z^{(1)},z^{(2)},z^{(3)},…,z^{(m)} \rbrace$
  - 利用生成器 $\tilde x^i = G(z^i)$ 输入噪声向量生成 $m$ 个反例 $\lbrace \tilde x^{(1)},\tilde x^{(2)},\tilde x^{(3)},…,\tilde x^{(m)} \rbrace$
  - 最大化 $\tilde V$ 更新判别器参数 $θ_D$：
    - $\tilde V = \frac{1}{m}\sum_{i=1}^{m} log D(x^i) + \frac{1}{m}\sum_{i=1}^{m} log (1-D(\tilde x^i))$
    - $θ_D := θ_D - \eta \nabla \tilde V(θ_D)$
- 训练生成器（G）的过程，循环 $1$ 次：
  - 从先验分布 $P_{prior}(x)$ 中抽样 $m$个噪声向量 $\lbrace z^{(1)},z^{(2)},z^{(3)},…,z^{(m)} \rbrace$
  - 最小化 $\tilde V$ 更新生成器参数 $θ_G$：
    - $\require{cancel}\tilde{V}=\cancel{\frac{1}{m}\sum_{i=1}^m\log D(x^i)}+\frac{1}{m}\sum_{i=1}^m\log(1-D(G(z^i)))$
    - $θ_G := θ_G - \eta \nabla \tilde V(θ_G)$

而 WGAN 的算法修改如下：

初始化一个由 $θ_D$ 决定的 $D$ 和由 $θ_G$ 决定的 $G$；
循环迭代训练过程：
- 训练判别器（D）的过程，循环 $k$ 次：
  - 从真实分布 $P_{data}(x)$ 中抽样 $m$个正例 $\lbrace x^{(1)},x^{(2)},x^{(3)},…,x^{(m)} \rbrace$
  - 从先验分布 $P_{prior}(x)$ 中抽样 $m$个噪声向量 $\lbrace z^{(1)},z^{(2)},z^{(3)},…,z^{(m)} \rbrace$
  - 利用生成器 $\tilde x^i = G(z^i)$ 输入噪声向量生成 $m$ 个反例 $\lbrace \tilde x^{(1)},\tilde x^{(2)},\tilde x^{(3)},…,\tilde x^{(m)} \rbrace$
  - 最大化 $\tilde V$ 更新判别器参数 $θ_D$：
    - $\tilde{V}=\frac{1}{m}\sum_{i=1}^mD(x^i)-\frac{1}{m}\sum_{i=1}^mD(\tilde{x}^i)$
    - $θ_D := θ_D - \eta \nabla \tilde V(θ_D)$
    - 更新参数后，截断参数；
- 训练生成器（G）的过程，循环 $1$ 次：
  - 从先验分布 $P_{prior}(x)$ 中抽样 $m$个噪声向量 $\lbrace z^{(1)},z^{(2)},z^{(3)},…,z^{(m)} \rbrace$
  - 最小化 $\tilde V$ 更新生成器参数 $θ_G$：
    - $\require{cancel}\tilde{V}=\cancel{\frac{1}{m}\sum_{i=1}^m\log D(x^i)}-\frac{1}{m}\sum_{i=1}^mD(G(z^i))$
    - $θ_G := θ_G - \eta \nabla \tilde V(θ_G)$

尤其需要注意的是，判别器的输出不再需用 sigmoid 函数了！并且需要训练 $k$ 次的判别器，然后只训练一次生成器。

改进 WGAN

在基础的 WGAN 中，我们通过 weight clipping 的方法来实现对判别器 D 的 $1-Lipschitz$ 的等效限制。$1-Lipschitz $ 函数有一个特性：当一个函数是 $1-Lipschitz$ 函数时，它的梯度的 norm 将永远小于等于 $1$。

$D\in\text{1-Lipschitz}\ \ \ \ \leftrightarrow\ \ \ \ ||\nabla_xD(x)||\le 1 ~~\text{for all x}$

此时 WGAN 的优化目标是在 $1-Lipschitz$ 中挑一个函数作为判别器 D。

而 Improved WGAN 则是这样：

$\begin{align} W(P_{data},P_G)=\max_{D}\{E_{x\sim P_{data} }[D(x)]-E_{x\sim P_G}[D(x)] \\ -\lambda\int_x\max(0,||\nabla_xD(x)||-1)dx\} \end{align}$

也就是说，现在我们寻找判别器的函数集不再是 $1-Lipschitz$ 中的函数了，而是任意函数。但是后面增加了一项惩罚项。这个惩罚项就能够让选中的判别器函数倾向于是一个“对输入梯度为 1 的函数”。这样也能实现类似 weight clipping 的效果。

但与之前遇到的问题一样，求积分无法计算，所以我们用采样的方法去加这个惩罚项，即：

$\begin{align} W(P_{data},P_G)=\max_{D}\{E_{x\sim P_{data} }[D(x)]-E_{x\sim P_G}[D(x)]\\ -\lambda E_{x\sim P_{penalty} }[\max(0,||\nabla_xD(x)||-1)]\} \end{align}$

也就是说，在训练过程中，我们更倾向于得到一个判别器 D，它能对从 $P_{penalty}$ 中采样得到的每一个 $x$ 都能 $||\nabla_xD(x)||\le 1$

Improved WGAN 设计了一个特别的 $P_{penalty}$。它的产生过程如下:

从 $P_{data}$ 中采样一个点;
从 $P_G$ 中采样一个点;
将这两个点连线;
在连线之上在采样得到一个点，就是一个从 $P_{penalty}$ 采样的一个点。

重复上面的过程就能不断采样得到 $x∼P_{penalty}$。最终得到下图中的蓝色区域就可以看作是 $P_{penalty}$：

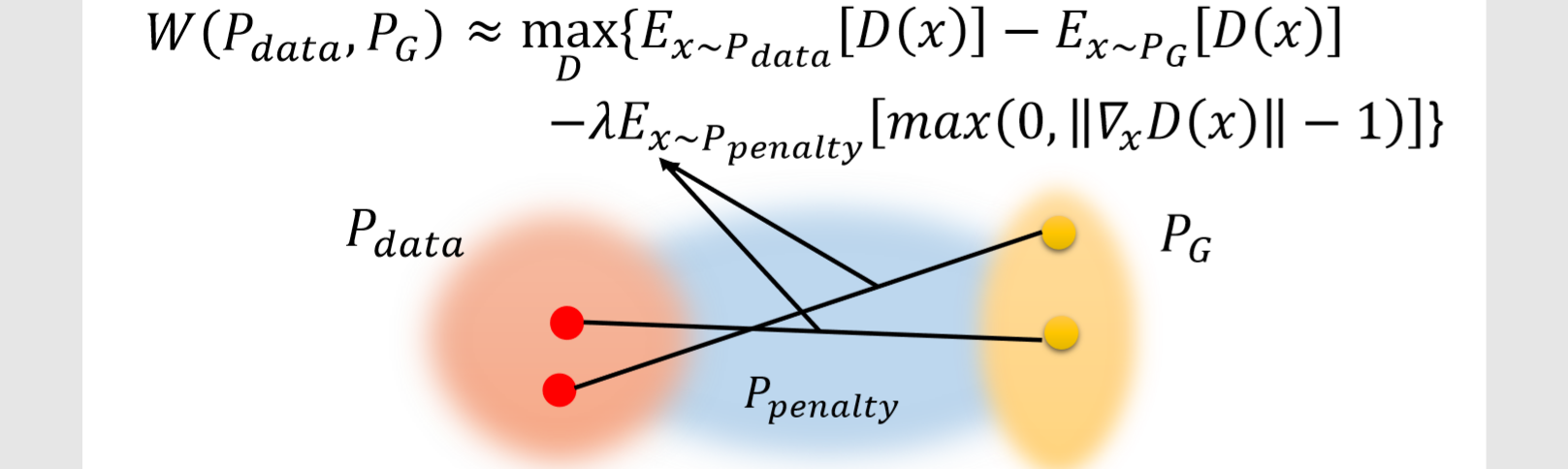
也就是说，我们采样的范围不是整个 $x$，只是 $P_G$ 和 $P_{data}$ 中间的空间中的一部分。再更进一步，Improved WGAN 真正做的事是这样：

$\begin{align} W(P_{data},P_G)=\max_{D}\{E_{x\sim P_{data} }[D(x)]-E_{x\sim P_G}[D(x)]\\ -\lambda E_{x\sim P_{penalty} }[(||\nabla_xD(x)||-1)^2]\} \end{align}$

这个惩罚项的目的是让梯度尽可能趋向于等于 1。即当梯度大于 1 或小于 1 时都会受到惩罚。而原来的惩罚项仅仅在梯度大于 1 时受到惩罚而已。

这样做是有好处的，就像我们在SVM中强调最大类间距离一样，虽然有多个可以将数据区分开的分类面，但我们希望找到不但能区分数据，还能让区分距离最大的那个分类面。这里这样做的目的是由于可能存在多个判别器，我们想要找到的那个判别器应该有一个“最好的形状”。

一个“好”的判别器应该在 $P_{data}$ 附近是尽可能大，要在 $P_G$ 附近尽可能小。也就是说处于 $P_{data}$ 和$P_G$之间的 $P_{penalty}$ 区域应该有一个比较“陡峭”的梯度。但是这个陡峭程度是有限制的，这个限制就是 1！

生成对抗网络系列文章（2）

前言

回顾传统 GAN 算法

F Divergence (F-Divergence)

Fenchel 共轭(Fenchel Conjugate)

F-Divergence GAN

WGAN

基础 WGAN

改进 WGAN

推荐阅读

CATALOG

FEATURED TAGS

FRIENDS