特殊应用：人脸识别和神经风格转换

GitHub项目传送门

欢迎Star

本篇博客有大量公式演示，不推荐使用手机查看

什么是人脸识别？(What is face recognition?)

人脸识别的相关文献中，常见到两个概念：人脸验证(face verification)和人脸识别(face recognition)。

• 人脸验证：
  • Input：图片、名字/ID；
  • Output：输入的图片是否是对应的人；
  • 1 to 1 问题。

• 人脸识别(Recognition)：

  • 拥有一个具有K个人的数据库；
  • 输入一副人脸图片；
  • 如果图片是任意这K个人中的一位，则输出对应人的ID。
  • 1 to K 问题

One-Shot学习(One-shot learning)

对于大多数的人脸识别系统都存在的一个问题就是one shot learning：就是说数据库中每个人的训练样本只包含一张照片，然后训练一个CNN模型来进行人脸识别，若数据库有K个人，则CNN模型输出softmax层就是K维的。

但是One-shot learning的性能并不好，其包含了两个缺点：

• 每个人只有一张图片，训练样本少，构建的CNN网络不够健壮。
• 若数据库增加另一个人，输出层softmax的维度就要发生变化，相当于要重新构建CNN网络，使模型计算量大大增加，不够灵活。

所以我们不能以传统的方法来实现识别系统。

Similarity 函数：

为了能够让人脸识别系统实现一次学习，需要让神经网络学习 Similarity 函数：

• $d(img1, img2)$：两幅图片之间的差异度
• 输入：两幅图片

• 输出：两者之间的差异度，阈值$\tau$，它是一个超参数：

  • 如果 $d(img1, img2) ⩽ \tau$ ，则输出“$same$”;
  • 如果 $d(img1, img2) > \tau$ ，则输出“$different$”.

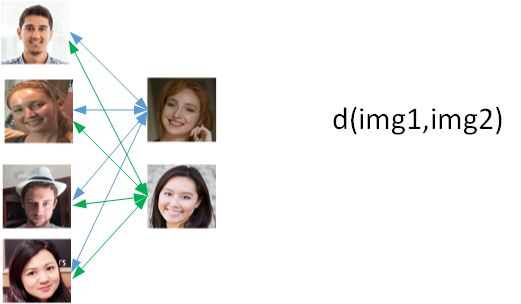
对于人脸识别系统，通过将输入的人脸图片与数据库中所拥有的图片成对输入Similarity函数，两两对比，则可解决one shot problem。如果有新的人加入团队，则只需将其图片添加至数据库即可。

Siamese 网络(Siamese network)

利用Siamese 网络来实现 Similarity 函数。

若一张图片经过一般的CNN网络（包括CONV层、POOL层、FC层），最终得到全连接层FC，该FC层可以看成是原始图片的编码encoding，表征了原始图片的关键特征。这个网络结构我们称之为Siamese network。也就是说每张图片经过Siamese network后，由FC层每个神经元来表征。

简单理解就是普通CNN去掉最后的softmax层

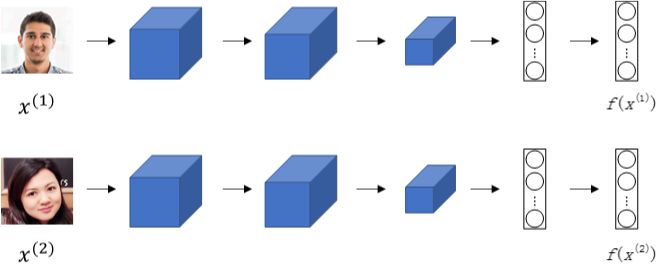
上图中，两幅图片的编码分别用$f(x^{(1)})$，$f(x^{(2)})$表示。

两张图片 $x^{(1)}$ 和 $x^{(2)}$ 的相似度函数可由各自FC层 $f(x^{(1)})$ 与 $f(x^{(2)})$ 之差的范数来表示：

$$d(x^{(1)},x^{(2)})=||f(x^{(1)})-f(x^{(2)})||^2$$

不同图片，运行相同的卷积神经网络。我们的目标就是利用梯度下降算法，不断调整网络参数，使得属于同一人的图片之间 $d(x^{(1)},x^{(2)})$ 很小，而不同人的图片之间 $d(x^{(1)},x^{(2)})$ 很大。

• 若 $x^{(i)}$ ， $x^{(j)}$ 是同一个人，则 $||f(x^{(1)})-f(x^{(2)})||^2$ 较小

• 若 $x^{(i)}$ ， $x^{(j)}$ 不是同一个人，则 $||f(x^{(1)})-f(x^{(2)})||^2$ 较大

详情参见DeepFace论文：Yaniv Taigman, Ming Yang, Marc’Aurelio Ranzato, Lior Wolf (2014).DeepFace: Closing the gap to human-level performance in face verification

Triplet 损失(Triplet Loss)

如何通过学习神经网络的参数，得到优质的人脸图片的编码？方法之一就是定义 Triplet 损失函数，并在其之上运用梯度下降。

1. 学习目标 ：

为了使用Triplet 损失函数，我们需要比较成对的图像（三元组术语），Triplet Loss需要每个样本包含三张图片：靶目标(Anchor)、正例(Positive)、反例(Negative)：

• Anchor (A)： 目标图片；
• Positive(P)：与Anchor 属于同一个人的图片；
• Negative(N)：与Anchor不属于同一个人的图片。

我们希望上一小节构建的CNN网络的Anchor输出编码 $f(A)$ 接近 Positive的输出编码$f(P)$ ；而对于Anchor 和Negative，我们希望他们编码（分别是$f(A)$，$f(N)$）的差异大一些。所以我们的目标以编码差的范数来表示为：

$$d(A,P)=||f(A) - f(P)||^{2} ⩽ ||f(A) - f(N)||^{2} = d(A,N)$$

也就是：

$$||f(A) - f(P)||^{2} - ||f(A) - f(N)||^{2} ⩽ 0$$

上述函数存在一个坏的情况，当 $f(A)=f(P)=f(N)=0$ 时，也就是神经网络学习到的函数总是输出 0 时，或者 $f(A)=f(P)=f(N)$ 时，也满足上面的公式，但却不是我们想要的目标结果。

所以为了防止出现这种情况，我们对上式进行修改，使得两者差要小于一个较小的负数：

$$||f(A) - f(P)||^{2} - ||f(A) - f(N)||^{2} ⩽ - \alpha$$

一般将 $\alpha$ 写成 $+\alpha$ ，称为“$margin$”，类似与支持向量机中的margin，即：

$$||f(A) - f(P)||^{2} - ||f(A) - f(N)||^{2} + \alpha ⩽ 0$$

2. 定义Triplet 损失函数：

Triplet 损失函数的定义基于三张图片：Anchor、Positive、Negative。

$$L(A,P,N) = \max (||f(A) - f(P)||^{2} - ||f(A) - f(N)||^{2} + \alpha, \ 0)$$

这个max函数的作用就是，只要你能达到这个目标 $||f(A) - f(P)||^{2} - ||f(A) - f(N)||^{2} + \alpha ⩽ 0$ ，那么损失函数就是0。只要你能使画绿色下划线部分小于等于0，只要你能达到这个目标，那么这个例子的损失就是0。

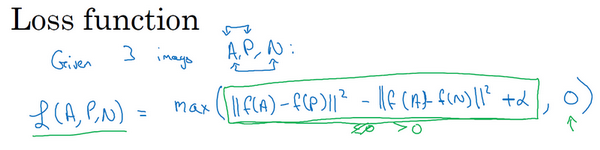
3. cost function为：

相应地，对于$m$组训练样本，cost function为：

$$J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)})$$

关于训练样本，必须保证同一人包含多张照片，否则无法使用这种方法。例如10k张照片包含1k个不同的人脸，则平均一个人包含10张照片。这个训练样本是满足要求的。

4. 三元组$(A,P,N)$的选择:

在训练的过程中，如果我们随机地选择图片构成三元组$(A,P,N)$，那么对于下面的条件是很容易满足的：

$$d(A,P) + \alpha ⩽ d(A,N)$$

所以，为了更好地训练网络，我们需要选择那些训练有“难度”的三元组，也就是选择的三元组满足：

$$d(A,P) \approx d(A,N)$$

• 算法将会努力使得 $d(A,N)$ 变大，或者使得 $d(A,N) + \alpha$ 变小，从而使两者之间至少有一个 $\alpha$ 的间隔；
• 增加学习算法的计算效率，避免那些太简单的三元组。

详情见论文：Florian Schroff, Dmitry Kalenichenko, James Philbin (2015).FaceNet: A Unified Embedding for Face Recognition and Clustering

下面给出一些A，P，N的例子：

总结就是，通过将anchor图片和positive图片和negative图片组成一个个三元组，然后通过Triplet 损失函数不断训练网络，让代价函数$J$不断变小，最后让网络学习到一种编码，使得如果两个图片是同一个人，那么它们的$d$就会很小，如果两个图片不是同一个人，它们的$d$就会很大。

这一领域的一个实用操作就是下载别人的预训练模型，而不是一切都要从头开始。

面部验证与二分类(Face verification and binary classification)

除了构造triplet loss来解决人脸识别问题之外，还可以使用二分类结构。做法是将两个siamese网络组合在一起，将各自的编码层输出经过一个逻辑输出单元，该神经元使用sigmoid函数，输出 1 则表示识别为同一人，输出 0 则表示识别为不同人。结构如下：

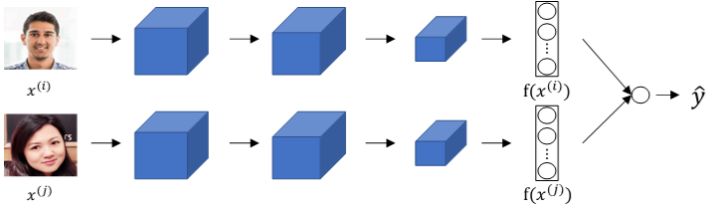
每组训练样本包含两张图片，每个siamese网络结构和参数完全相同。这样就把人脸识别问题转化成了一个二分类问题。引入逻辑输出层参数$w$和$b$，输出 $\hat y$ 表达式为：

$$\hat y=\sigma(\sum_{k=1}^Kw_k|f(x^{(i)})_ k-f(x^{(j)})_ k|+b)$$

其中， $f(x^{(i)})$ 代表图片 $x^{(i)}$ 的编码，下标 $k$ 代表选择N维编码向量中的第 $k$ 个元素。

其中参数 $w_k$ 和 $b$ 都是通过梯度下降算法迭代训练得到。 g $\hat y$ 的另外一种表达式为：

$$\hat y=\sigma(\sum_{k=1}^Kw_k\frac{(f(x^{(i)})_ k-f(x^{(j)})_ k)^2}{f(x^{(i)})_ k+f(x^{(j)})_ k}+b)$$

上式被称为 $\chi$ 方公式，也叫 $\chi$ 方相似度。

在实际的人脸验证系统中，可以使用预计算的方式在训练时就将数据库每个模板的编码层输出 $f(x)$ 保存下来。只要计算测试图片的siamese网络，得到的 $f(x^{(i)})$ 直接与存储的模板 $f(x^{(j)})$ 进行下一步的逻辑输出单元计算即可，节省计算时间。

什么是神经风格转换？(What is neural style transfer?)

为了描述如何实现神经网络迁移，我将使用来$C$表示内容图像，$S$表示风格图像，$G$表示生成的图像.

什么是深度卷积网络？(What are deep ConvNets learning?)

在进行神经风格迁移之前，我们先来从可视化的角度看一下卷积神经网络每一层到底是什么样子？它们各自学习了哪些东西。

典型的CNN网络如下所示：

我们希望看到不同层的隐藏单元的计算结果。依次对各个层进行如下操作：

• 在当前层挑选一个隐藏单元；
• 遍历训练集，找到最大化地激活了该运算单元的图片或者图片块；
• 对该层的其他运算单元执行操作。

首先来看第一层隐藏层，遍历所有训练样本，找出让该层激活函数输出最大的9块图像区域；然后再找出该层的其它单元（不同的滤波器通道）激活函数输出最大的9块图像区域；最后共找9次，得到9 x 9的图像如下所示，其中每个3 x 3区域表示一个运算单元。

可以看出，第一层隐藏层一般检测的是原始图像的边缘和颜色阴影等简单信息。

继续看CNN的更深隐藏层，随着层数的增加，捕捉的区域更大，特征更加复杂，从边缘到纹理再到具体物体.

详情见论文：Zeiler and Fergus.,2013,Visualizing and Understanding Convolutional Networks

代价函数(Cost function)

为了实现神经风格迁移，我们需要为生成的图片定义一个代价函数。

对于神经风格迁移，我们的目标是由内容图片$C$和风格图片$S$，生成最终的风格迁移图片$G$。

神经风格迁移生成图片$G$的cost function由两部分组成：$C$与$G$的相似程度和$S$与$G$的相似程度：

$$J(G)=\alpha \cdot J_{content}(C,G)+\beta \cdot J_{style}(S,G)$$

• $J_{content}(C, G)$ 代表生成图片$G$的内容和内容图片$C$的内容的相似度；
• $J_{style}(S,G)$ 代表生成图片$G$的内容和风格图片$S$的内容的相似度；
• $\alpha$、$\beta$ 两个超参数用来表示以上两者之间的权重。

神经风格迁移的基本算法流程是：首先令$G$为随机像素点，然后使用梯度下降算法，不断修正$G$的所有像素点，使得 $J(G)$ 不断减小，从而使$G$逐渐有$C$的内容和$G$的风格，如下图所示。

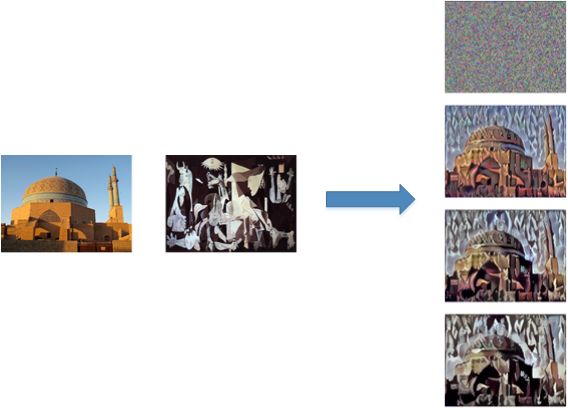
神经风格迁移算法是基于Leon Gatys， Alexandra Ecker和Matthias Bethge的这篇论文：Leon A. Gatys, Alexander S. Ecker, Matthias Bethge, (2015). A Neural Algorithm of Artistic Style

内容代价函数(Content cost function)

我们先来看 $J(G)$ 的第一部分 $J_{content}(C,G)$ ，它表示内容图片$C$与生成图片$G$之间的相似度。

使用的CNN网络是之前训练好的模型，例如Alex-Net。$C$，$S$，$G$共用相同模型和参数。首先，需要选择合适的层数$l$来计算 $J_{content}(C,G)$ 。

• 如果 $l$ 太小，则$G$与$C$在像素上会非常接近，没有迁移效果；
• 如果 $l$ 太深，则$G$上某个区域将直接会出现$C$中的物体。
• 因此， $l$ 既不能太浅也不能太深，一般选择网络中间层。

我们令$a^{[l] (C)}$这个和$a^{[l] (G)}$，代表这两个图片$C$和$G$的层的激活函数值。如果这两个激活值相似，那么就意味着两个图片的内容相似

相应的 $J_{content}(C,G)$ 的表达式为：

$$J_{content}(C,G)=\frac12||a^{[l] (C)}-a^{[l] (G)}||^2$$

$a^{[l] (C)}$ 与$ a^{[l] (G)} $越相似，则 $J_{content}(C,G)$ 越小。方法就是使用梯度下降算法，不断迭代修正$G$的像素值，使 $J_{content}(C,G)$ 不断减小。

这就是两个图片之间$l$层激活值差值的平方和.

风格代价函数(Style cost function)

首先，什么是图片间的风格：利用CNN网络模型，图片的风格可以定义成第 $l$ 层隐藏层不同通道间激活函数的乘积（相关性）

例如我们选取第 $l$ 层隐藏层，其各通道使用不同颜色标注，如下图所示。因为每个通道提取图片的特征不同，比如 1 通道（红色）提取的是图片的垂直纹理特征，2 通道（黄色）提取的是图片的橙色背景特征。而相关性大小的含义就是，如假设中，图片出现垂直纹理特征的区域显示橙色可能的大小。

也就是说，计算不同通道的相关性，反映了原始图片特征间的相互关系，从某种程度上刻画了图片的“风格”。

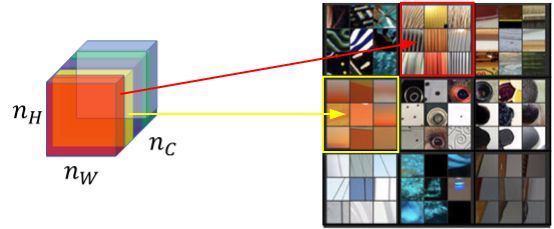
现在，定义图片的风格矩阵(style matrix)为：

$$G_{kk'}^{[l]}=\sum_{i=1}^{n_H^{[l]}}\sum_{j=1}^{n_W^{[l]}}a_{ijk}^{[l]}a_{ijk'}^{[l]}$$

• $[l]$ 表示第 $l$ 层隐藏层.
• $i$、$j$、$k$分别代表激活值的高、宽、通道，$k$，$k’$分别表示不同通道，所以$l$层的高度和宽度分别为：$n_H^{[l]}$，$n_W^{[l]}$，通道数为 $n_C^{[l]}$。
• 令 $a^{[l]}_{i,j,k}$ 表示在$(i,j,k)$位置的激活值；
• $G^{[l]}$ 是一个 $n_{c}^{l}\times n_{c}^{l}$ 大小的矩阵，计算的是第 $l$ 层隐藏层不同通道对应的所有激活函数输出和：
• 若两个通道之间相似性高，则对应的 $G_{kk’}^{[l]}$ 较大；若两个通道之间相似性低，则对应的 $G_{kk’}^{[l]}$ 较小。

因此，可以得出下列两条公式，分别代表同时对风格图$S$和生成图像$G$进行运算得到的输出和：

$$G_{kk'}^{[l] (S)} = \sum\limits_{i=1}^{n_{h}^{[l]}}\sum\limits_{j=1}^{n_{w}^{[l]}}a_{i,j,k}^{[l] (S)}a_{i,j,k'}^{[l] (S)}$$ $$G_{kk'}^{[l] (G)} = \sum\limits_{i=1}^{n_{h}^{[l]}}\sum\limits_{j=1}^{n_{w}^{[l]}}a_{i,j,k}^{[l] (G)}a_{i,j,k'}^{[l] (G)}$$

• 风格矩阵 $G_{kk’}^{[l] (S)}$ 表征了风格图片$S$第 $l$ 层隐藏层的“风格”。
• 相应地，生成图片$G$也有 $G_{kk’}^{[l] (G)}$ 。

那么， $G_{kk’}^{[l] (S)}$ 与 $G_{kk’}^{[l] (G)}$ 越相近，则表示$G$的风格越接近$S$。

因此定义风格矩阵的代价函数：

$$J_{style}^{[l]}(S, G) = \dfrac{1}{2n_{h}^{[l]}n_{w}^{[l]}n_{c}^{[l]}}||G^{[l] (S)} - G^{[l] (G)} ||_ {F}^{2} = \dfrac{1}{2n_{h}^{[l]}n_{w}^{[l]}n_{c}^{[l]}}\sum_{k}\sum_{k'}(G_{kk'}^{[l] (S)} - G_{kk'}^{[l] (G)})^{2}$$

这将得到这两个矩阵之间的误差，因为它们是矩阵，所以在这里加一个F（Frobenius范数），这实际上是计算两个矩阵对应元素相减的平方的和，我们把这个式子展开，从$k$和$k’$开始作它们的差，把对应的式子写下来，然后把得到的结果都加起来，然后乘以一个归一化常数$\dfrac{1}{2n_{h}^{[l]}n_{w}^{[l]}n_{c}^{[l]}}$，再在外面加一个平方。但是一般情况下你不用写这么多，一般我们只要将它乘以一个超参数$β$就行 。

定义完 $J_{style}(S,G)^{[l]}$ 之后，我们的目标就是使用梯度下降算法，不断迭代修正$G$的像素值，使 $J_{style}(S,G)^{[l]}$ 不断减小。

值得一提的是，以上我们只比较计算了一层隐藏层 $l$ 。为了提取的“风格”更多，也可以使用多层隐藏层，然后相加，表达式为：

$$J_{style}(S,G)=\sum_l\lambda^{[l]}\cdot J^{[l]}_{style}(S,G)$$

其中， $\lambda^{[l]}$ 表示累加过程中各层 $J^{[l]}_{style}(S,G)$ 的权重系数，为超参数。

根据以上两小节的推导，最终的cost function为：

$$J(G)=\alpha \cdot J_{content}(C,G)+\beta \cdot J_{style}(S,G)$$

一维到三维推广(1D and 3D generalizations of models)

在我们上面学过的卷积中，多数是对图形应用2D的卷积运算。同时，我们所应用的卷积运算还可以推广到1D和3D的情况。

1. 首先介绍2D卷积的规则：

• 输入图片维度：14 x 14 x 3
• 滤波器尺寸：5 x 5 x 3，滤波器个数：16
• 输出图片维度：10 x 10 x 16

1. 将2D卷积推广到1D卷积，举例来介绍1D卷积的规则：

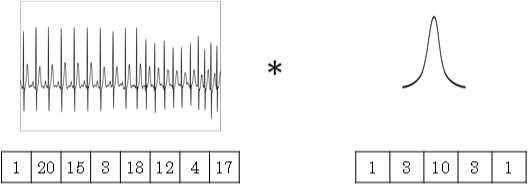
• 输入时间序列维度：14 x 1
• 滤波器尺寸：5 x 1，滤波器个数：16
• 输出时间序列维度：10 x 16

1. 对于3D卷积，举例来介绍其规则：

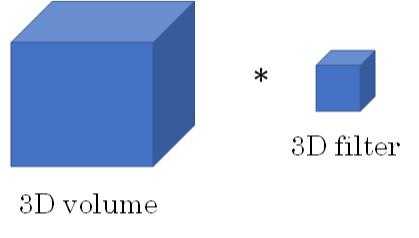
• 输入3D图片维度：14 x 14 x 14 x 1
• 滤波器尺寸：5 x 5 x 5 x 1，滤波器个数：16
• 输出3D图片维度：10 x 10 x 10 x 16

本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：黄钢的博客 ，同时保持文章内容的完整和以上声明信息！

---

• Previous
  目标检测
• Next
  Caffe Mnist 实例