超参数调试、Batch 正则化和程序框架

GitHub项目传送门

欢迎Star

超参数调试处理(Tuning process)

目前已经讲到过的超参数中，重要程度依次是（仅供参考）：

最重要：
- 学习率 $α$；
其次重要：
- $β$：动量衰减参数，常设置为 $0.9$；
- #hidden units：各隐藏层神经元个数；
- mini-batch 的大小；
再次重要：
- $β1$，$β2$，$ϵ$：Adam 优化算法的超参数，常设为 $0.9$、$0.999$、$10^{-8}$；
- #layers：神经网络层数;
- decay_rate：学习衰减率；

如何选择和调试超参数？传统的机器学习中，我们对每个参数等距离选取任意个数的点，然后，分别使用不同点对应的参数组合进行训练，最后根据验证集上的表现好坏，来选定最佳的参数。例如有两个待调试的参数，分别在每个参数上选取 5 个点，这样构成了 5x5=25 中参数组合，如下图所示：

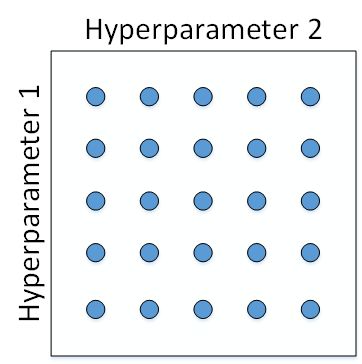
但是在深度神经网络模型中，我们一般不采用这种均匀间隔取点的方法，比较好的做法是使用随机选择。对于上面这个例子，我们随机选择 25 个点，作为待调试的超参数，如下图所示：

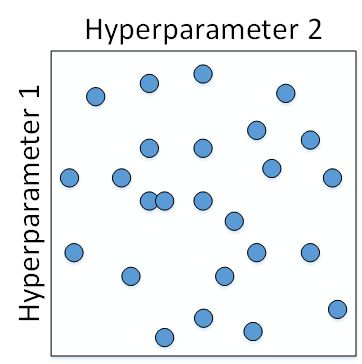
在实际应用中完全不知道哪个参数更加重要的情况下，随机采样的方式能有效解决这一问题，但是均匀采样做不到这点。

为了得到更精确的最佳参数，我们应该继续对选定的区域进行由粗到细的采样(coarse to fine sampling scheme)。也就是放大表现较好的区域，再对此区域做更密集的随机采样。例如，对下图中右下角的方形区域再做 25 点的随机采样，以获得最佳参数。

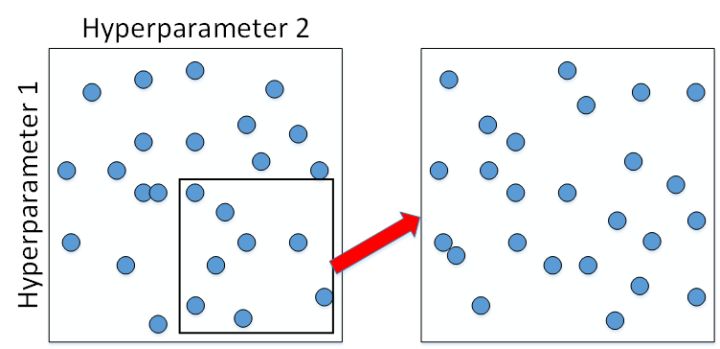
为超参数选择合适的范围(Using an appropriate scale to pick hyperparameters)

在超参数选择的时候，一些超参数是在一个范围内进行均匀随机取值，如隐藏层神经元结点的个数、隐藏层的层数等。但是有一些超参数的选择做均匀随机取值是不合适的，这里需要按照一定的比例在不同的小范围内进行均匀随机取值。

对于学习率 $α$，待调范围是$[0.0001, 1]$。如果使用均匀随机采样，那么有 90% 的采样点分布在$[0.1, 1]$之间，只有 10% 分布在$[0.0001, 0.1]$之间。这在实际应用中是不太好的，因为最佳的 $\alpha$ 值可能主要分布在$[0.0001, 0.1]$之间，而$[0.1, 1]$范围内 $\alpha$ 值效果并不好。因此我们更关注的是区间$[0.0001, 0.1]$，应该在这个区间内细分更多刻度。

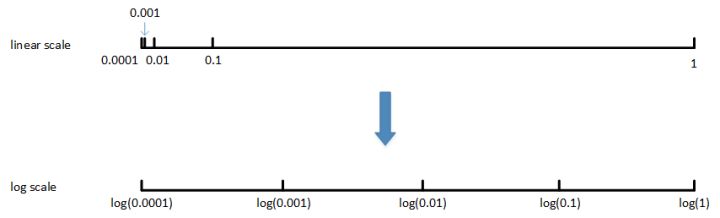
一般解法是，如果线性区间为$[a, b]$，令$m=log(a)$，$n=log(b)$，则对应的$log$区间为$[m,n]$。对$log$区间的$[m,n]$进行随机均匀采样，然后得到的采样值$r$，最后反推到线性区间，即 $10^r$ 。 $10^r$ 就是最终采样的超参数。

m = np.log10(a)
n = np.log10(b)
r = np.random.rand()
r = m + (n-m)*r
r = np.power(10,r)

对于 $β$，一般 $\beta$ 的取值范围在$[0.9, 0.999]$之间，那么 $1-\beta$ 的取值范围就在$[0.001, 0.1]$之间。那么直接对 $1-\beta$ 在$[0.001, 0.1]$区间内进行$log$变换即可。
- 至于为什么这么做：假设 $\beta$ 从 0.9000 变化为 0.9005 ，那么 $\frac{1}{1-\beta} $基本没有变化。但假设 $\beta$ 从 0.9990 变化为 0.9995 ，那么 $\frac{1}{1-\beta}$ 前后差别 1000。 $\beta$ 越接近 1 ，指数加权平均的个数越多，变化越大。所以对 $\beta$ 接近1的区间，应该采集得更密集一些。

超参数调试实践:Pandas vs. Caviar(Hyperparameters tuning in practice: Pandas vs. Caviar)

如何搜索参数的过程大概分两种重要的思想流派，或者说人们通常采用的两种重要但不同的方法。

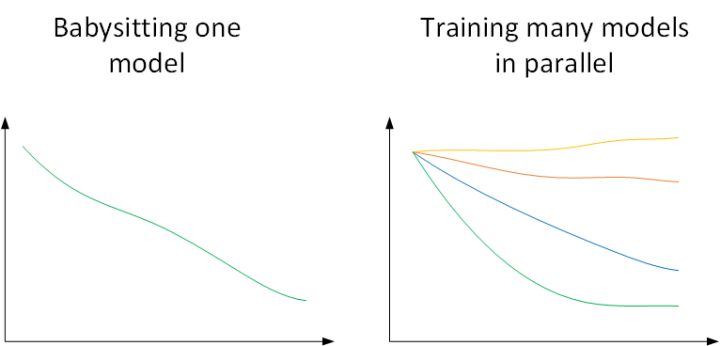
根据你所拥有的计算资源来决定你训练模型的方式：
- Panda（熊猫方式）：在在线广告设置或者在计算机视觉应用领域有大量的数据，但受计算能力所限，同时试验大量模型比较困难。可以采用这种方式：试验一个或一小批模型，初始化，试着让其工作运转，观察它的表现，不断调整参数；
- Caviar（鱼子酱方式）：拥有足够的计算机去平行试验很多模型，尝试很多不同的超参数，选取效果最好的模型；
考虑到数据的变化或者服务器的变更等因素，建议每隔几个月至少一次，重新测试或评估超参数，来获得实时的最佳模型；

正则化网络中的激活函数(Normalizing activations in a network)

Batch 归一化 会使你的参数搜索问题变得很容易，使神经网络对超参数的选择更加稳定，超参数范围会很庞大，工作效果也很好，也容易使你很容易地训练甚至是深层网络。

标准化输入可以提高训练的速度。方法是对训练数据集进行归一化的操作，即将原始数据减去其均值 $\mu$ 后，再除以其方差 $\sigma^2$ 。但是标准化输入只是对输入进行了处理，那么对于神经网络，又该如何对各隐藏层的输入进行标准化处理呢？

我们也可以用同样的思路处理隐藏层的激活值 $a[l]$，以加速 $W[l+1]$和 $b[l+1]$的训练。在实践中，经常选择标准化 $Z[l]$：

$\mu = \frac{1}{m} \sum_i z^{(i)}$ $\sigma^2 = \frac{1}{m} \sum_i {(z_i - \mu)}^2$ $z_{norm}^{(i)} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2 + \epsilon}}$

其中，$m$ 是单个 mini-batch 所包含的样本个数，$ϵ$ 是为了防止分母为零，通常取 $10^{-8}$

这样，我们使得所有的输入 $z^{(i)}$均值为 0，方差为 1。但我们不想让隐藏层单元总是含有平均值 0 和方差 1，也许隐藏层单元有了不同的分布会更有意义。因此，我们计算

$\tilde z^{(i)} = \gamma z^{(i)}_{norm} + \beta$

其中，$γ $和 $β$ 都是模型的学习参数，所以可以用各种梯度下降算法来更新 $γ$ 和 $β$ 的值，如同更新神经网络的权重一样。

通过对 $γ$ 和 $β$ 的合理设置，可以让 $\tilde z^{(i)}$ 的均值和方差为任意值。这样，我们对隐藏层的 $z^{(i)}$进行标准化处理，用得到的 $\tilde z^{(i)}$替代 $z^{(i)}$。

设置 $γ$ 和 $β$ 的原因 是：如果各隐藏层的输入均值在靠近 0 的区域，即处于激活函数的线性区域，不利于训练非线性神经网络，从而得到效果较差的模型。因此，需要用 $γ$ 和 $β$ 对标准化后的结果做进一步处理。

在神经网络中融入Batch Norm(Fitting Batch Norm into a neural network)

对于 $L$层神经网络，经过 Batch Normalization 的作用，整体流程如下：

值得注意的是，因为Batch Norm对各隐藏层 $Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$ 有去均值的操作，所以这里的常数项 $b^{[l]}$ 可以消去，其数值效果完全可以由 $\tilde Z^{[l]}$ 中的 $\beta$ 来实现。因此，我们在使用Batch Norm的时候，可以忽略各隐藏层的常数项$ b^{[l]}$ 。在使用梯度下降算法时，分别对$ W^{[l]}$， $\beta^{[l]}$ 和 $\gamma^{[l]}$ 进行迭代更新。

除了传统的梯度下降算法之外，还可以使用我们之前介绍过的动量梯度下降、RMSprop或者Adam等优化算法。

Batch Norm 起作用的原因(Why does Batch Norm work?)

Batch Normalization 效果很好的原因有以下两点：

通过对隐藏层各神经元的输入做类似的标准化处理，提高神经网络训练速度；
可以使前面层的权重变化对后面层造成的影响减小，即前面的$W$的变化对后面$W$造成的影响很小，整体网络更加健壮。

关于第二点，如果实际应用样本和训练样本的数据分布不同（如下图所示，提供的所有猫的训练样本都是黑猫，但是测试样本里却是什么颜色的猫都有，模型测试的结果有可能不尽人意）。

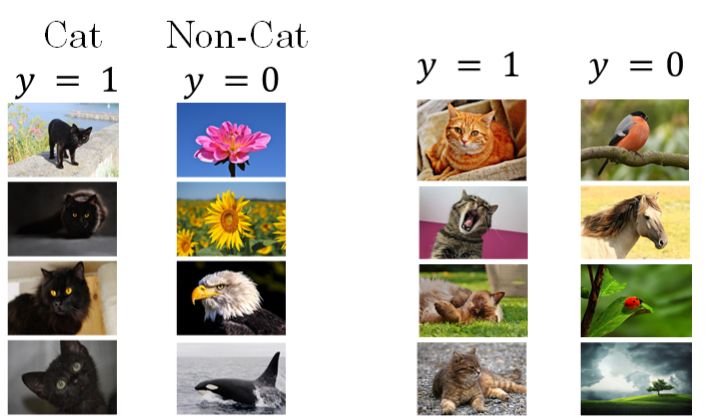
我们称发生了“Covariate Shift”。这种情况下，一般要对模型进行重新训练。Batch Normalization 的作用就是减小 Covariate Shift 所带来的影响，让模型变得更加健壮，鲁棒性(Robustness)更强。

Batch Norm减少了各层 $W^{[l]}$ 、$B^{[l]}$ 之间的耦合性，让各层更加独立，实现自我训练学习的效果。也就是说，如果输入发生covariate shift，那么因为Batch Norm的作用，对个隐藏层输出 $Z^{[l]}$ 进行均值和方差的归一化处理， $W^{[l]}$ 和 $B^{[l]}$ 更加稳定，使得原来的模型(识别黑猫)也有不错的表现。针对上面这个黑猫的例子，如果我们使用深层神经网络，使用Batch Norm，那么该模型对花猫的识别能力(新能力)应该也是不错的。

另外，Batch Normalization 也 起到微弱的正则化(regularization)效果。因为在每个 mini-batch 而非整个数据集上计算均值和方差，只由这一小部分数据估计得出的均值和方差会有一些噪声，因此最终计算出的 $\tilde z^{(i)}$也有一定噪声。类似于 dropout，这种噪声会使得神经元不会再特别依赖于任何一个输入特征。

最后，不要将 Batch Normalization 作为正则化的手段，而是当作加速学习的方式。正则化只是一种非期望的副作用，Batch Normalization 解决的还是反向传播过程中的梯度问题（梯度消失和爆炸）。

在测试数据上使用 Batch Norm(Batch Norm at test time)

训练过程中，Batch Norm是对单个mini-batch进行操作的，但在测试过程中，如果是单个样本，该如何使用Batch Norm进行处理呢？

首先，回顾一下训练过程中Batch Norm的主要过程：

$\mu = \frac{1}{m} \sum_i z^{(i)}$ $\sigma^2 = \frac{1}{m} \sum_i {(z_i - \mu)}^2$ $z_{norm}^{(i)} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2 + \epsilon}}$ $\tilde z^{(i)} = \gamma z^{(i)}_{norm} + \beta$

其中， $\mu$ 和 $\sigma^2$ 是对单个mini-batch中所有$m$个样本求得的。在测试过程中，如果只有一个样本，求其均值和方差是没有意义的，就需要对 $\mu$ 和 $\sigma^2$ 进行估计。这个时候一般使用指数加权平均(exponentially weighted average)的方法来预测测试过程中单个样本的$\mu$ 和 $\sigma^2$

指数加权平均的做法很简单，对于第 $l$ 层隐藏层，考虑所有mini-batch在该隐藏层下的 $\mu^{[l]} $和 $\sigma^{2[l]}$ ，然后用指数加权平均的方式来预测得到当前单个样本的 $\mu^{[l]}$ 和 $\sigma^{2[l]}$ 。这样就实现了对测试过程单个样本的均值和方差估计。最后，再利用训练过程得到的 $\gamma$ 和 $\beta$ 值计算出各层的 $\tilde z^{(i)}$ 值。

Softmax 回归(Softmax Regression)

目前为止，介绍的分类例子都是二分类问题：神经网络输出层只有一个神经元，表示预测输出 $\hat y$是正类的概率 $ P(y = 1|x) $ ，$\hat y > 0.5$ 则判断为正类，反之判断为负类。

对于 多分类问题 ，用 C 表示种类个数，则神经网络输出层，也就是第 L 层的单元数量 $ n^{[L]} = C $ 。每个神经元的输出依次对应属于该类的概率，即 $ P(y = c|x), c = 0, 1, .., C-1 $ 。有一种 Logistic 回归的一般形式，叫做 Softmax 回归，可以处理多分类问题。

对于 Softmax 回归模型的输出层，即第 L 层，有：

$Z^{[L]} = W^{[L]}a^{[L-1]} + b^{[L]}$

$for\ \ i\ \ in\ \ range(L)$，有：

$a^{[L]}_i = \frac{e^{Z^{[L]}_i}}{\sum^C_{i=1}e^{Z^{[L]}_i}}$

为输出层每个神经元的输出，对应属于该类的概率，满足：

$\sum^C_{i=1}a^{[L]}_i = 1$

所有的 $a^{[L]}_i$ ，即 $\hat y$ ，维度为(C, 1)。

训练 Sotfmax 分类器(Training a softmax classifier)

一个直观的例子：

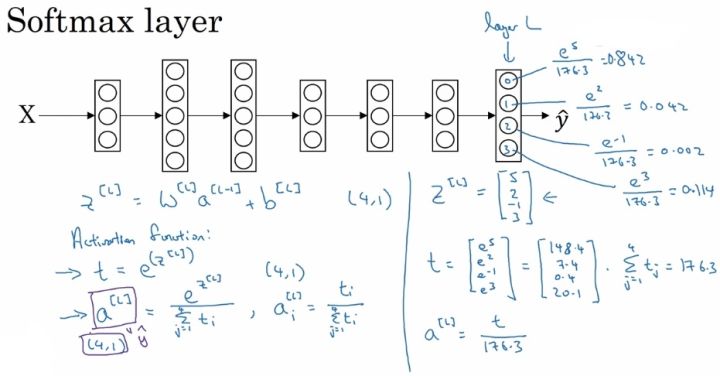
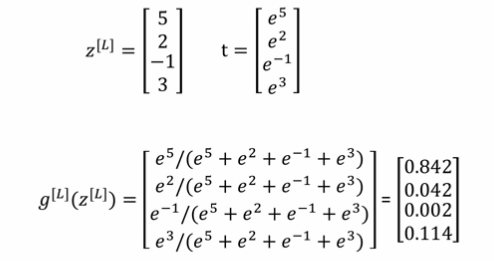
损失函数和成本函数:

定义 损失函数 为：

$L(\hat y, y) = -\sum^C_{j=1}y_jlog\hat y_j$

当 i 为样本真实类别，则有：

$y_j = 0, j \ne i$

因此，损失函数可以简化为：

$L(\hat y, y) = -y_ilog\hat y_i = log \hat y_i$

所有 m 个样本的成本函数为：

$J = \frac{1}{m}\sum^m_{i=1}L(\hat y, y)$

所以为了最小化Loss function，我们的目标就变成了使得 $\hat y_{j}$ 的概率尽可能的大。

也就是说，这里的损失函数的作用就是找到你训练集中的真实的类别，然后使得该类别相应的概率尽可能地高，这其实是最大似然估计的一种形式。

多分类的 Softmax 回归模型与二分类的 Logistic 回归模型只有输出层上有一点区别。经过不太一样的推导过程，仍有

$dZ^{[L]} = A^{[L]} - Y$

反向传播过程的其他步骤也和 Logistic 回归的一致。

本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：黄钢的博客，同时保持文章内容的完整和以上声明信息！

"deeplearning.ai-Class2-Week3"