优化算法

GitHub项目传送门

欢迎Star

Mini-batch梯度下降(Mini-batch gradient descent)

batch 梯度下降法（批梯度下降法，我们之前一直使用的梯度下降法）是最常用的梯度下降形式，即同时处理整个训练集。其在更新参数时使用所有的样本来进行更新。

对整个训练集进行梯度下降法的时候，我们必须处理整个训练数据集，然后才能进行一步梯度下降，即每一步梯度下降法需要对整个训练集进行一次处理，如果训练数据集很大的时候，处理速度就会比较慢。

Mini-Batch 梯度下降法（小批量梯度下降法）每次同时处理单个的 mini-batch，其他与 batch 梯度下降法一致。

假设总的训练样本个数 m=5000000，其维度为 $(n_x,m)$ 。将其分成5000个子集，每个mini-batch含有1000个样本。我们将每个mini-batch记为 $X^{{t}}$ ，其维度为 $(n_x,1000)$ 。相应的每个mini-batch的输出记为 $Y^{{t}}$ ，其维度为 $(1,1000)$ ，且 $t=1,2,\cdots,5000$ 。

这里顺便总结一下我们遇到的神经网络中几类字母的上标含义：

$X^{(i)}$ ：第 $i$ 个样本
$Z^{[l]}$ ：神经网络第 $l$ 层网络的线性输出
$X^{{t}},Y^{{t}}$ ：第 $t$ 组 mini-batch

for t=1,…,T {

$\ \ \ \ Forward\ Propagation$

$\ \ \ \ Compute Cost Function$

$\ \ \ \ Backward Propagation$

$\ \ \ \ W:=W-\alpha\cdot dW$

$\ \ \ \ b:=b-\alpha\cdot db$

}

经过 $T$ 次循环之后，所有 $m$ 个训练样本都进行了梯度下降计算。这个过程，我们称之为经历了一个 epoch。对于 batch 梯度下降法来说，一个 epoch 只进行一次梯度下降算法；而 Mini-Batches 梯度下降法，一个epoch会进行 $T$ 次梯度下降算法。

batch 梯度下降法和 Mini-batch 梯度下降法代价函数的变化趋势如下，使用 batch 梯度下降法，成本是随着迭代次数不断减少的，而使用 Mini-Batches 梯度下降法，呈现震荡下降的趋势。

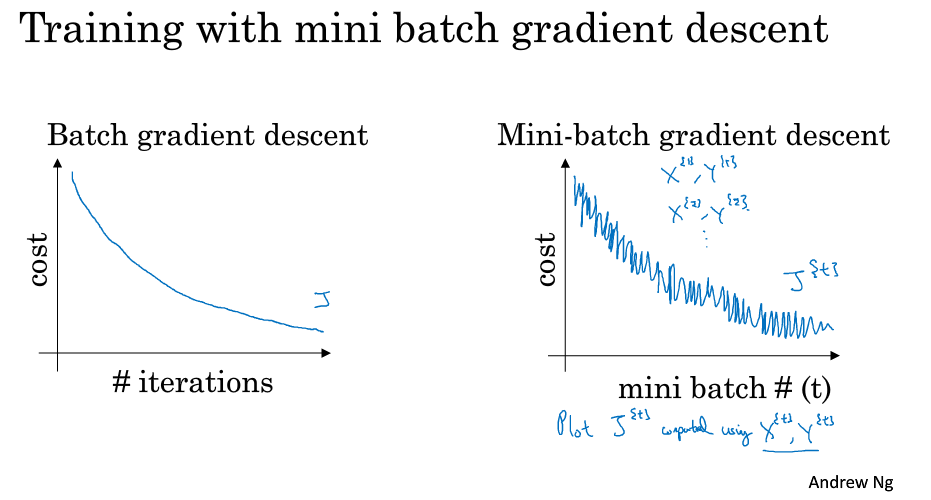
之所以出现细微振荡的原因是不同的mini-batch之间是有差异的。例如可能第一个子集 $(X^{{1}},Y^{{1}})$ 是好的子集，而第二个子集 $(X^{{2}},Y^{{2}})$ 包含了一些噪声 noise。出现细微振荡是正常的。

batch 的不同大小(size)带来的影响

mini-batch 的大小为 1，即是 随机梯度下降法(stochastic gradient descent)，每个样本都是独立的 mini-batch；
- 对每一个训练样本执行一次梯度下降，但是丢失了向量化带来的计算加速；
- Cost function总体的趋势向最小值的方向下降，但是无法到达全局最小值点，呈现波动的形式。
mini-batch 的大小为 m（数据集大小），即是 batch 梯度下降法；
- 对所有m个训练样本执行一次梯度下降，每一次迭代时间较长；
- Cost function 总是向减小的方向下降
Mini-batch梯度下降的大小为 $1 - m$ 之间：
- 可以实现快速学习，也应用了向量化带来的好处；
- 且 Cost function 的下降处于前两者之间。

决定的变量之一是 mini-batch 的大小（m 是训练集的大小）。

mini-batch 大小的选择：

如果训练样本的大小比较小，如 m ⩽ 2000 时，选择 batch 梯度下降法；
如果训练样本的大小比较大，选择 mini-batch 梯度下降法。为了和计算机的信息存储方式相适应，代码在 mini-batch 大小为 2 的幂次时运行要快一些。典型的大小为 $2^6$、$2^7$、…、$2^9$；
mini-batch 的大小要符合 CPU/GPU 内存。

获得 mini-batch 的步骤

将数据集打乱；
按照既定的大小分割数据集；

其中打乱数据集的代码：

m = X.shape[1]
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))

指数加权平均(Exponentially weighted averages)

指数加权平均(Exponentially Weight Average) 是一种常用的序列数据处理方式，计算公式为：

$s_t = \begin{cases} Y_1, &t = 1 \\\ \beta Y_t + (1-\beta)s_{t-1}, &t > 1 \end{cases}$

其中 $Y_t$ 为 $t$ 下的实际值，$s_t$ 为 $t$ 下加权平均后的值，$β$ 为权重值。

指数加权平均数在统计学中被称为“指数加权移动平均值”。

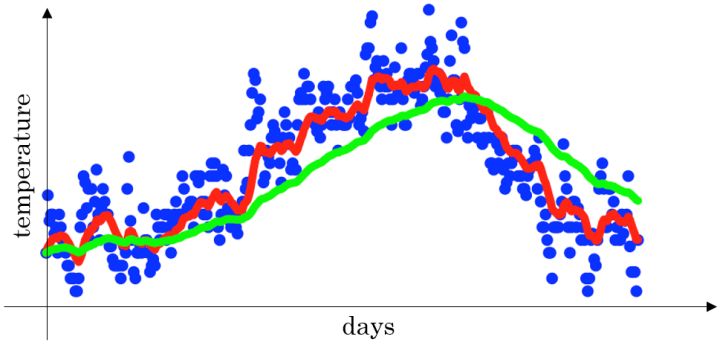
比如：给定一个时间序列，例如伦敦一年每天的气温值，图中蓝色的点代表真实数据，对于一个即时的气温值。

取权重值 $β = 0.9$ ，根据求得的值可以得到图中的红色曲线，它反映了气温变化的大致趋势。
当取权重值 $β=0.98$ 时，可以得到图中更为平滑的绿色曲线。
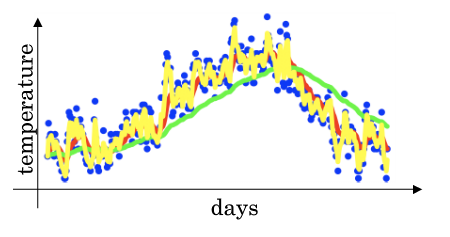
而当取权重值 $β=0.5$ 时，得到图中噪点更多的黄色曲线。

$β$ 越大相当于求取平均利用的天数越多，曲线自然就会越平滑而且越滞后。

理解指数加权平均(Understanding Exponentially weighted averages)

当 $β$ 为 0.9 时:

第1天的气温与第0天的气温有关：$v_{1} = 0.9v_{0} + 0.1\theta_{1}$ 第2天的气温与第1天的气温有关：$v_{2} = 0.9v_{1} + 0.1\theta_{2}$ 第3天的气温与第2天的气温有关：$v_{3} = 0.9v_{2} + 0.1\theta_{3}$ 以此类推：$…$ 第100天的气温与第99天的气温有关：$v_{100} = 0.9v_{99} + 0.1\theta_{100}$

展开：

$v_{100} = 0.1\theta_{100} + 0.1 * 0.9\theta_{99} + 0.1 * {(0.9)}^2\theta_{98} + ...$

其中 $θ_i$ 指第 $i$ 天的实际数据。所有 $θ$ 前面的系数（不包括 0.1，比如$\theta_{100}$的指数为 1 ，$\theta_{99}$的指数为 0.9……）相加起来为 1 或者接近于 1，这些系数被称作 偏差修正(Bias Correction)。

我们将指数加权平均公式的一般形式写下来：

$V_{t} = \beta V_{t-1} + (1-\beta) \theta_{t}=(1-\beta) \theta_{t}+(1-\beta)·\beta· \theta_{t}+(1-\beta)·\beta^2· \theta_{t}+...+(1-\beta)·\beta^{t-1}·\theta_{1}+\theta^tV^0$

观察上面这个式子， $\theta_t,\theta_{t-1},\theta_{t-2},\cdots,\theta_1$ 原始数据值， $(1-\beta)$,$(1-\beta)\beta$,$(1-\beta)\beta^2$,$\cdots$,$(1-\beta)\beta^{t-1}$ 是类似指数曲线，从右向左，呈指数下降的。 $V_t$ 的值就是这两个子式的点乘，将原始数据值与衰减指数点乘，相当于做了指数衰减，离得越近，影响越大，离得越远，影响越小，衰减越厉害。

根据函数极限的一条定理：

${\lim_{\epsilon\to 0}}(1 - \epsilon)^{\frac{1}{\epsilon}} = \frac{1}{e} \approx 0.368$

在我们的例子中，$1-\varepsilon=\beta=0.9$。

当 $β$ 为 0.9 时，$\frac{1}{1-\beta}=10$，可以当作把过去 10 天的气温指数加权平均作为当日的气温，第10天的气温指数已经下降到了当天的 1/3 左右，再往前数（过去第11天，12天，13……）气温指数就可以忽略了。
同理，当 $β$ 为 0.98 时，$\frac{1}{1-\beta}=50$，可以把过去 50 天的气温指数加权平均作为当日的气温。

因此，在计算当前时刻的平均值时，只需要前一天的平均值和当前时刻的值。

$v_t = \beta v_{t-1} + (1 - \beta)\theta_t$

考虑到代码，只需要不断更新 $v$ 即可：

$v := \beta v + (1 - \beta)\theta_t$

指数平均加权并 不是最精准 的计算平均数的方法，你可以直接计算过去 10 天或 50 天的平均值来得到更好的估计，但缺点是保存数据需要占用更多内存，执行更加复杂，计算成本更加高昂。

指数加权平均数公式的好处之一在于它只需要一行代码，且占用极少内存，因此 效率极高，且节省成本 。

指数加权平均的偏差修正(Bias correction in exponentially weighted averages)

在我们执行指数加权平均的公式时，当 $\beta=0.98$ 时，我们得到的并不是图中的绿色曲线，而是下图中的紫色曲线，其起点比较低。

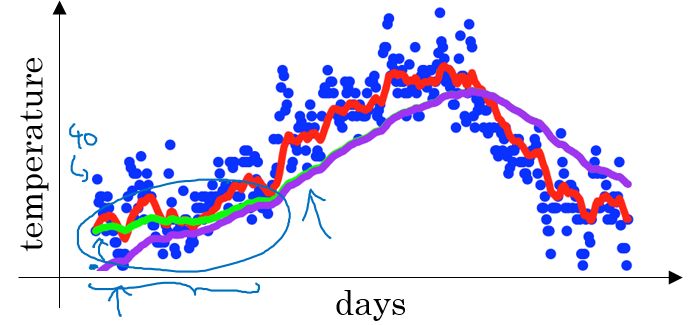
原因是：

$v_0 = 0$ $v_1 = 0.98v_0 + 0.02\theta_1$

如果第一天的值为如 40 ，则 $v_{1}=0.02\times40=8$ ，得到的值要远小于实际值,因此，$v_1$ 仅为第一个数据的 0.02（或者说 $1-β$），后面几天的情况也会由于初值引起的影响，均低于实际均值。

因此，我们修改公式为

$\frac{v\_t}{1-\beta^t} = \beta v_{t-1} + (1 - \beta)\theta_t$

偏差修正得到了绿色的曲线，在开始的时候，能够得到比紫色曲线更好的计算平均的效果。随着 $t$ 逐渐增大， $\beta^{t}$ 接近于 0，所以后面绿色的曲线和紫色的曲线逐渐重合了。

momentum梯度下降(Gradient descent with momentum)

动量梯度下降(Gradient Descent with Momentum) 的基本思想就是计算梯度的指数加权平均数，并利用该梯度来更新权重。

在我们优化 Cost function 的时候，以下图所示的函数图为例：

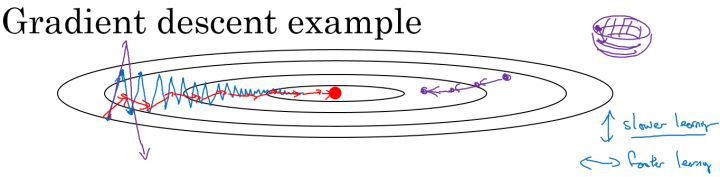
在利用梯度下降法来最小化该函数的时候，每一次迭代所更新的代价函数值如图中蓝色线所示在上下波动，而这种幅度比较大波动，减缓了梯度下降的速度，而且我们只能使用一个较小的学习率来进行迭代。

如果用较大的学习率，结果可能会如紫色线一样偏离函数的范围，所以为了避免这种情况，只能用较小的学习率。

但是我们又希望在如图的纵轴方向梯度下降的缓慢一些，不要有如此大的上下波动，在横轴方向梯度下降的快速一些，使得能够更快的到达最小值点，而这里用动量梯度下降法既可以实现，如红色线所示。

具体算法如下：

for l = 1, .. , L：

$v_{dW^{[l]}} = \beta v_{dW^{[l]}} + (1 - \beta) dW^{[l]}$ $v_{db^{[l]}} = \beta v_{db^{[l]}} + (1 - \beta) db^{[l]}$ $W^{[l]} := W^{[l]} - \alpha v_{dW^{[l]}}$ $b^{[l]} := b^{[l]} - \alpha v_{db^{[l]}}$

其中，将动量衰减参数 $β$ 设置为 0.9 是超参数的一个常见且效果不错的选择。当 $β$ 被设置为 0 时，显然就成了 batch 梯度下降法。

算法本质解释：

在对应上面的计算公式中，将Cost function想象为一个碗状，想象从顶部往下滚球，其中：

$dw$，$db$ 想象成球的加速度；而 $v_{dw}$、$v_{db}$ 相当于速度。

小球在向下滚动的过程中，因为加速度的存在速度会变快，但是由于 β 的存在，其值小于 1，可以认为是摩擦力，所以球不会无限加速下去。

RMSprop

RMSProp（Root Mean Square Prop，均方根） 算法是在对梯度进行指数加权平均的基础上，引入平方和平方根。每次迭代训练过程中，其权重W和常数项b的更新表达式为，具体过程为（省略了 $l$）：

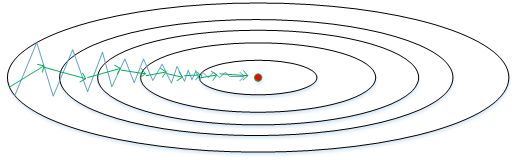
$s_{dw} = \beta s_{dw} + (1 - \beta)(dw)^2$ $s_{db} = \beta s_{db} + (1 - \beta)(db)^2$ $w := w - \alpha \frac{dw}{\sqrt{s_{dw} + \epsilon}}$ $b := b - \alpha \frac{db}{\sqrt{s_{db} + \epsilon}}$

从图中可以看出，梯度下降（蓝色折线）在垂直方向($b$)上振荡较大，在水平方向($W$)上振荡较小，表示在b方向上梯度较大，即 $db$ 较大，而在W方向上梯度较小，即 $dW$ 较小。因此，上述表达式中 $S_b$ 较大，而 $S_W$ 较小。在更新W和b的表达式中，变化值 $\frac{dW}{\sqrt{S_W}}$ 较大，而 $\frac{db}{\sqrt{S_b}}$ 较小。也就使得W变化得多一些，$b$ 变化得少一些。即加快了 $W$ 方向的速度，减小了 $b$ 方向的速度，减小振荡，实现快速梯度下降算法，其梯度下降过程如绿色折线所示。总得来说，就是如果哪个方向振荡大，就减小该方向的更新速度，从而减小振荡。

还有一点需要注意的是为了避免RMSprop算法中分母为零，通常可以在分母增加一个极小的常数 $\varepsilon$ ：

$\frac{dw}{\sqrt{s_{dw} + \epsilon}}$ $\frac{db}{\sqrt{s_{db} + \epsilon}}$

其中， $\varepsilon=10^{-8}$ ，或者其它较小值。

Adam优化算法(Adam optimization algorithm)

Adam (Adaptive Moment Estimation) 优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法，通常有超越二者单独时的效果。具体过程如下（省略了 $l$）：

首先进行初始化：

$V_{dW} = 0, V_{dW} = 0, S_{db} = 0, S_{db} = 0$

用每一个 mini-batch 计算 $dW$、$db$，第 $t$ 次迭代时：

$V_{dW} = \beta_1 V_{dW} + (1 - \beta_1) dW$ $V_{db} = \beta_1 V_{db} + (1 - \beta_1) db$ $S_{dW} = \beta_2 S_{dW} + (1 - \beta_2) {(dW)}^2$ $S_{db} = \beta_2 S_{db} + (1 - \beta_2) {(db)}^2$

一般使用 Adam 算法时需要计算偏差修正：

$V^{corrected}_{dW} = \frac{V_{dW}}{1-{\beta_1}^t}$ $V^{corrected}_{db} = \frac{V_{db}}{1-{\beta_1}^t}$ $S^{corrected}_{dW} = \frac{S_{dW}}{1-{\beta_2}^t}$ $S^{corrected}_{db} = \frac{S_{db}}{1-{\beta_2}^t}$

所以，更新 $W$、$b$ 时有：

$W := W - \alpha \frac{V^{corrected}_{dW}}{ {\sqrt{S^{corrected}_{dW}} + \epsilon}}$ $b := b - \alpha \frac{V^{corrected}_{db}}{ {\sqrt{S^{corrected}_{db}} + \epsilon}}$

（可以看到 Andrew 在这里 $ϵ$ 没有写到平方根里去，和他在 RMSProp 中写的不太一样。考虑到 $ϵ$ 所起的作用，我感觉影响不大）

超参数的选择

Adam 优化算法有很多的超参数，其中

学习率 $α$：需要尝试一系列的值，来寻找比较合适的；
$β_1$：常用的缺省值为 0.9；
$β_2$：Adam 算法的作者建议为 0.999；
$ϵ$：不重要，不会影响算法表现，Adam 算法的作者建议为 $10^{-8}$；

$β_1$、$β_2$、$ϵ$ 通常不需要调试。

学习率衰减(Learning rate decay)

如果设置一个固定的学习率 $α$，在最小值点附近，由于不同的 batch 中存在一定的噪声，因此不会精确收敛，而是始终在最小值周围一个较大的范围内波动。

而如果随着时间慢慢减少学习率 $α$ 的大小，在初期 $α$ 较大时，下降的步长较大，能以较快的速度进行梯度下降；而后期逐步减小 $α$ 的值，即减小步长，有助于算法的收敛，更容易接近最优解。

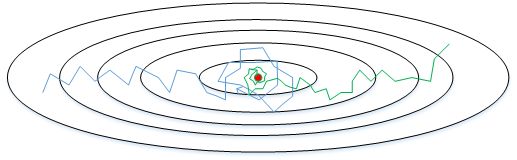
下图中，蓝色折线表示使用恒定的学习因子 $\alpha$ ，由于每次训练 $\alpha $相同，步进长度不变，在接近最优值处的振荡也大，在最优值附近较大范围内振荡，与最优值距离就比较远。
绿色折线表示使用不断减小的 $\alpha$ ，随着训练次数增加， $\alpha$ 逐渐减小，步进长度减小，使得能够在最优值处较小范围内微弱振荡，不断逼近最优值。

最常用的学习率衰减方法：

$\alpha = \frac{1}{1 + decay_{rate} * epoch_{num} } * \alpha_0$

其中，decay_rate为衰减率（超参数），epoch_num为将所有的训练样本完整过一遍的次数。

指数衰减：

$\alpha = 0.95^{ epoch_{num} } * \alpha\_0$

其他：

$\alpha = \frac{k}{\sqrt{epoch_{num} } } * \alpha_0$

离散下降:

对于较小的模型，也有人会在训练时根据进度手动调小学习率。

局部最优问题(The problem of local optima)

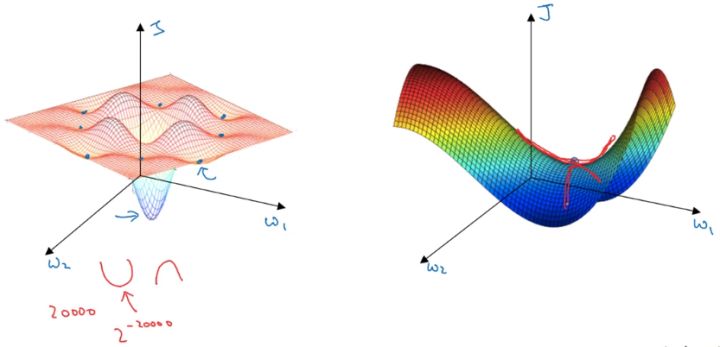
在低维度的情形下，我们可能会想象到一个Cost function 如左图所示，存在一些局部最小值点，在初始化参数的时候，如果初始值选取的不得当，会存在陷入局部最优点的可能性。

但是，如果我们建立一个高维度的神经网络。通常梯度为零的点，并不是如左图中的局部最优点，而是右图中的鞍点（叫鞍点是因为其形状像马鞍的形状）, 鞍点(saddle) 是函数上的导数为零，但不是轴上局部极值的点。

类似马鞍状的plateaus会降低神经网络学习速度。Plateaus是梯度接近于零的平缓区域，如下图所示。在plateaus上梯度很小，前进缓慢，到达鞍点需要很长时间。到达鞍点后，由于随机扰动，梯度一般能够沿着图中绿色箭头，离开鞍点，继续前进，只是在plateaus上花费了太多时间。

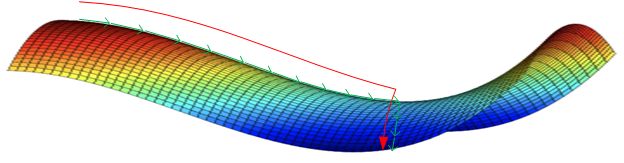
结论：

在训练较大的神经网络、存在大量参数，并且成本函数被定义在较高的维度空间时，困在极差的局部最优中是不大可能的；
鞍点附近的平稳段会使得学习非常缓慢，而这也是动量梯度下降法、RMSProp 以及 Adam 优化算法能够加速学习的原因，它们能帮助尽早走出平稳段。

本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：黄钢的博客，同时保持文章内容的完整和以上声明信息！

"deeplearning.ai-Class2-Week2"