深度学习的实用层面

GitHub项目传送门

欢迎Star

本篇博客有大量公式演示，不推荐使用手机查看

训练、验证、测试集(Train / Dev / Test sets)

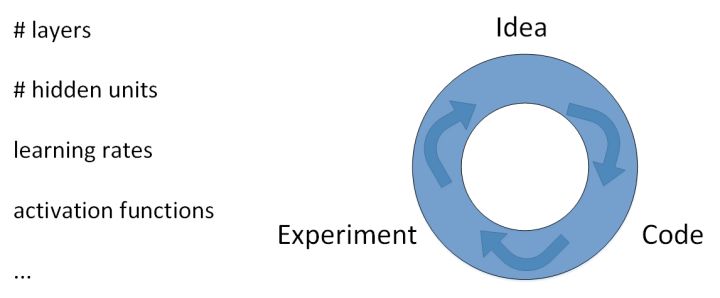
应用深度学习是一个典型的迭代过程。这个循环迭代的过程是这样的：

我们先有个想法Idea，先选择初始的参数值，构建神经网络模型结构；
然后通过代码Code的形式，实现这个神经网络；
最后，通过实验Experiment验证这些参数对应的神经网络的表现性能。

根据验证结果，我们对参数进行适当的调整优化，再进行下一次的Idea->Code->Experiment循环。通过很多次的循环，不断调整参数，选定最佳的参数值，从而让神经网络性能最优化。

对于一个需要解决的问题的样本数据，在建立模型的过程中，数据会被划分为以下几个部分：

训练集(train set)：用训练集对算法或模型进行训练过程；
验证集(development set)：利用验证集（又称为简单交叉验证集，hold-out cross validation set）进行 交叉验证 ，选择出最好的模型 ；
测试集(test set)：最后利用测试集对模型进行测试，获取模型运行的无偏估计 （对学习方法进行评估）。

在 小数据量 的时代，如 100、1000、10000 的数据量大小，可以将数据集按照以下比例进行划分：

无验证集的情况：70% / 30%；
有验证集的情况：60% / 20% / 20%；

而在如今的 大数据时代 ，对于一个问题，我们拥有的数据集的规模可能是百万级别的，所以验证集和测试集所占的比重会趋向于变得更小。

验证集的目的是为了验证不同的算法哪种更加有效，所以验证集只要足够大到能够验证大约 2-10 种算法哪种更好，而不需要使用 20% 的数据作为验证集。如百万数据中抽取 1 万的数据作为验证集就可以了。

测试集的主要目的是评估模型的效果，如在单个分类器中，往往在百万级别的数据中，我们选择其中 1000 条数据足以评估单个模型的效果。

100 万数据量：98% / 1% / 1%；
超百万数据量：99.5% / 0.25% / 0.25%（或者99.5% / 0.4% / 0.1%）

Tips:

建议验证集和测试集来自于同一个分布，这样可以使得机器学习算法变得更快；
如果不需要用无偏估计来评估模型的性能，则可以不需要测试集。

补充：交叉验证(cross validation)

交叉验证的基本思想是重复地使用数据；把给定的数据进行切分，将切分的数据集组合为训练集与测试集，在此基础上反复地进行训练、测试以及模型选择。

偏差、方差(Bias /Variance)

偏差(Bias)和方差(Variance):在传统的机器学习算法中，Bias和Variance是对立的，分别对应着欠拟合和过拟合，常常需要在Bias和Variance之间进行权衡。而在深度学习中，我们可以同时减小Bias和Variance，构建最佳神经网络模型。

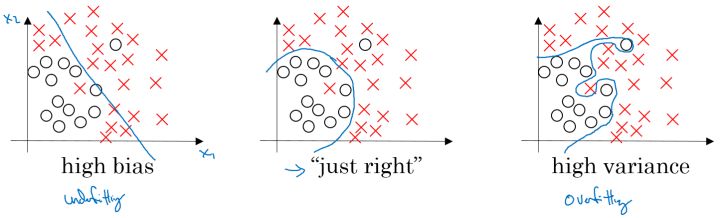
从图中我们可以看出，在欠拟合(underfitting)的情况下，出现高偏差(high bias)的情况；在过拟合(overfitting)的情况下，出现高方差(high variance)的情况。

在偏差-方差权衡的角度来讲，我们利用训练集对模型进行训练就是为了使得模型在训练集上使偏差最小化，避免出现欠拟合的情况；

但是如果模型设置的太复杂，虽然在训练集上偏差的值非常小，模型甚至可以将所有的数据点正确分类，但是当将训练好的模型应用在开发（验证）集上的时候，却出现了较高的错误率。这是因为模型设置的太复杂则没有排除一些训练集数据中的噪声，使得模型出现过拟合的情况，在开发（验证）集上出现高方差的现象。

“偏差-方差分解”(bias-variance decomposition)是解释学习算法泛化性能的一种重要工具。

泛化误差可分解为偏差、方差与噪声之和：

偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了 学习算法本身的拟合能力 ；
方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了 数据扰动所造成的影响 ；
噪声：表达了在当前任务上任何学习算法所能够达到的期望泛化误差的下界，即刻画了 学习问题本身的难度 。

偏差-方差分解说明，泛化性能 是由 学习算法的能力 、数据的充分性 以及 学习任务本身的难度 所共同决定的。给定学习任务，为了取得好的泛化性能，则需要使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。

看下面这个例子：

当训练出一个模型以后，如果：

训练集的错误率较小(1%)，而验证集的错误率却较大(11%)，说明模型存在较大方差，可能出现了过拟合，模型泛化能力不强，导致验证集识别率低；
训练集(15%)和开发集(16%)的错误率都较大，且两者相当，说明模型存在较大偏差，可能出现了欠拟合；
训练集错误率较大(15%)，且开发集的错误率(30%)远较训练集大，说明方差和偏差都较大，模型很差，这是最糟糕的情况，可以理解成某段区域是欠拟合的，某段区域是过拟合的；
训练集(0.5%)和开发集(1%)的错误率都较小，且两者的相差也较小，说明方差和偏差都较小，这个模型效果比较好。

应对方法

存在高偏差：

扩大网络规模，如添加隐藏层或隐藏单元数目；
寻找合适的网络架构，使用更大的 NN 结构；
花费更长时间训练。

存在高方差：

获取更多的数据；
正则化(regularization)；
寻找更合适的网络结构。

正则化(Regularization)

利用正则化(Regularization)来解决高方差(High variance)的问题，正则化是在成本函数(Cost function)中加入一项正则化项，惩罚模型的复杂度。

Logistic回归中的正则化

$J(w,b) = \frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})+\frac{\lambda}{2m}{||w||}^2_2$

L2 正则化：

$\frac{\lambda}{2m}{||w||}^2_2 = \frac{\lambda}{2m}\sum_{j=1}^{n_x}w^2_j = \frac{\lambda}{2m}w^Tw$

L1 正则化：

$\frac{\lambda}{2m}{||w||}_1 = \frac{\lambda}{2m}\sum_{j=1}^{n_x}{|w_j|}$

其中，λ 为 正则化因子 ，是需要调整的 超参数 。

由于 L1 正则化最后得到 w 向量中将存在大量的 0，使模型变得 稀疏化 ，因此 L2 正则化更加常用。

注意，lambda在 Python 中属于保留字，所以在编程的时候，用lambd代替这里的正则化因子。

神经网络中的正则化

对于神经网络，加入正则化的成本函数：

$J(w^{[1]}, b^{[1]}, ..., w^{[L]}, b^{[L]}) = \frac{1}{m}\sum_{i=1}^mL(\hat{y}^{(i)},y^{(i)})+\frac{\lambda}{2m}\sum_{l=1}^L{ {||w^{[l]}||}}^2_F$

因为 w 的大小为 ($n^{[l−1]}$, $n^{[l]}$)，因此

${ {||w^{[l]}||}}^2_F = \sum^{n^{[l-1]}}_{i=1}\sum^{n^{[l]}}_{j=1}(w^{[l]}_{ij})^2$

该矩阵范数被称为 弗罗贝尼乌斯范数(Frobenius Norm) ，所以神经网络中的正则化项被称为弗罗贝尼乌斯范数矩阵。

权重衰减(Weight decay)

在加入正则化项后，梯度变为（反向传播要按这个计算），它定义含有代价函数的导数和以及添加的正则项：

$dW^{[l]}= \frac{\partial L}{\partial w^{[l]}} +\frac{\lambda}{m}W^{[l]}$

代入梯度更新公式：

$W^{[l]} := W^{[l]}-\alpha dW^{[l]}$

可得：

$W^{[l]} := W^{[l]} - \alpha [\frac{\partial L}{\partial w^{[l]}} + \frac{\lambda}{m}W^{[l]}]$ $= W^{[l]} - \alpha \frac{\lambda}{m}W^{[l]} - \alpha \frac{\partial L}{\partial w^{[l]}}$ $= (1 - \frac{\alpha\lambda}{m})W^{[l]} - \alpha \frac{\partial L}{\partial w^{[l]}}$

其中，

$(1 - \frac{\alpha\lambda}{m})W^{[l]}<1$

会给原来的 $W^{[l]}$一个衰减的参数。所以 L2 正则化项也被称为 权重衰减(Weight Decay)。

为什么正则化有利于防止过拟合(Why regularization reduces overfitting?)

为什么正则化能够有效避免high variance，防止过拟合呢？下面我们通过几个例子说明。

还是之前那张图，从左到右，分别表示了欠拟合，刚好拟合，过拟合三种情况。

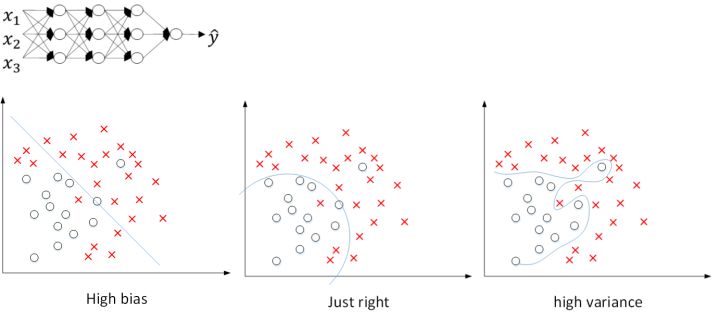
假如我们选择了非常复杂的神经网络模型，如上图左上角所示。在未使用正则化的情况下，我们得到的分类超平面可能是类似上图右侧的过拟合。但是，如果使用正则化因子，直观上理解，正则化因子 \lambda 设置的足够大的情况下，为了使代价函数最小化，权重矩阵 W 就会被设置为接近于0的值。则相当于消除了很多神经元的影响，那么图中的大的神经网络就会变成一个较小的网络。

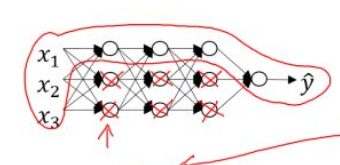
当然上面这种解释是一种直观上的理解，但是实际上隐藏层的神经元依然存在，但是他们的影响变小了，便不会导致过拟合。

数学解释

假设神经元中使用的激活函数为g(z) = tanh(z)（sigmoid 同理）。

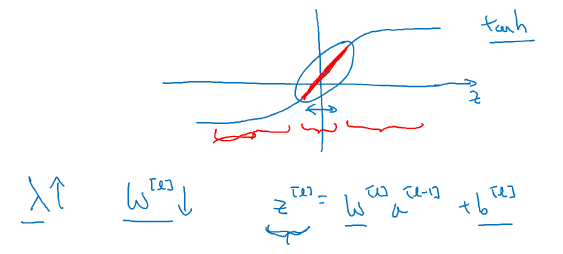
在加入正则化项后，当 $λ$ 增大，导致 $W^{[l]}$减小，$Z^{[l]} = W^{[l]}a^{[l-1]} + b^{[l]}$便会减小。由上图可知，在 $z$ 较小（接近于 0）的区域里，tanh(z)函数近似线性，所以每层的函数就近似线性函数，整个网络就成为一个简单的近似线性的网络，因此不会发生过拟合。

其他解释

在权值 $w^{[L]}$变小之下，输入样本 $X$ 随机的变化不会对神经网络模造成过大的影响，神经网络受局部噪音的影响的可能性变小。这就是正则化能够降低模型方差的原因。

dropout正则化(Dropout Regularization)

dropout（随机失活） ：是在神经网络的隐藏层为每个神经元结点设置一个随机消除的概率，保留下来的神经元形成一个结点较少、规模较小的网络用于训练。dropout 正则化较多地被使用在 计算机视觉(Computer Vision) 领域。

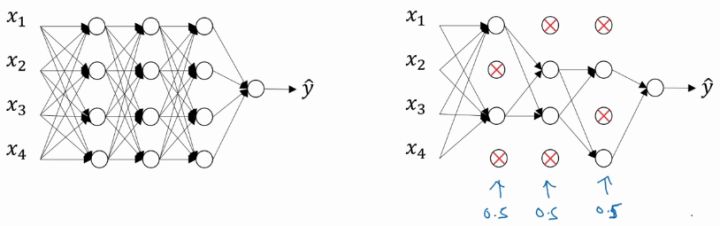
实现Dropout的方法：反向随机失活(Inverted dropout):

反向随机失活是实现 dropout 的方法。对第l层进行 dropout：

keep_prob = 0.8    # 设置神经元保留概率
dl = np.random.rand(al.shape[0], al.shape[1]) < keep_prob
al = np.multiply(al, dl)
al /= keep_prob

最后一步al /= keep_prob是因为 $a^{[l]}$中的一部分元素失活（相当于被归零），为了在下一层计算时不影响 $Z^{[l+1]} = W^{[l+1]}a^{[l]} + b^{[l+1]}$ 的期望值，因此 $W^{[l+1]}a^{[l]}$ 除以一个keep_prob,用来弥补 $Z^{[l+1]}$ 20%的损失。

假设第 $l$ 层有50个神经元，经过dropout后，有10个神经元停止工作，这样只有40神经元有作用。那么得到的 $a^{[l]}$ 只相当于原来的80%。scale up后，能够尽可能保持 $a^{[l]}$ 的期望值相比之前没有大的变化。

对于 $m$ 个样本，单次迭代训练时，随机删除掉隐藏层一定数量的神经元；然后，在删除后的剩下的神经元上正向和反向更新权重 $w$ 和常数项 $b$ ；接着，下一次迭代中，再恢复之前删除的神经元，重新随机删除一定数量的神经元，进行正向和反向更新 $w$ 和 $b$ 。不断重复上述过程，直至迭代训练完成。

注意，在 测试阶段不要使用 dropout ，因为那样会使得预测结果变得随机。

理解dropout(Understanding Dropout)

对于单个神经元，其工作是接收输入并产生一些有意义的输出。但是加入了 dropout 后，输入的特征都存在被随机清除的可能，所以该神经元不会再特别依赖于任何一个输入特征，即不会给任何一个输入特征设置太大的权重。

因此，通过传播过程，dropout 将产生和 L2 正则化相同的 收缩权重 的效果。

对于不同的层，设置的keep_prob也不同。一般来说，神经元较少的层，会设keep_prob为 1.0，而神经元多的层则会设置比较小的keep_prob，比如 0.8 甚至 0.5 。

dropout 的一大缺点是成本函数无法被明确定义。因为每次迭代都会随机消除一些神经元结点的影响，因此无法确保成本函数单调递减。

一般做法是，将所有层的keep_prob全设置为 1，再绘制cost function，即涵盖所有神经元，看J是否单调下降。下一次迭代训练时，再将keep_prob设置为其它值。

其他正则化方法(Other regularization methods)

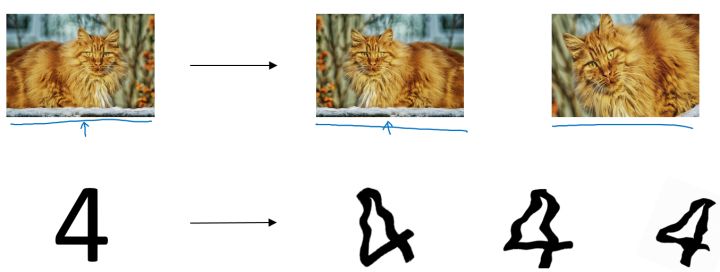
数据扩增(Data Augmentation)：通过图片的一些变换（翻转，局部放大后切割等），得到更多的训练集和验证集。

早停止法(Early Stopping)：一个神经网络模型随着迭代训练次数增加，train set error一般是单调减小的，而dev set error 先减小，之后又增大。也就是说训练次数过多时，模型会对训练样本拟合的越来越好，但是对验证集拟合效果逐渐变差，即发生了过拟合。因此将训练集和验证集进行梯度下降时的成本变化曲线画在同一个坐标轴内，在两者开始发生较大偏差时及时停止迭代，避免过拟合。这种方法的缺点是无法同时达成偏差和方差的最优。

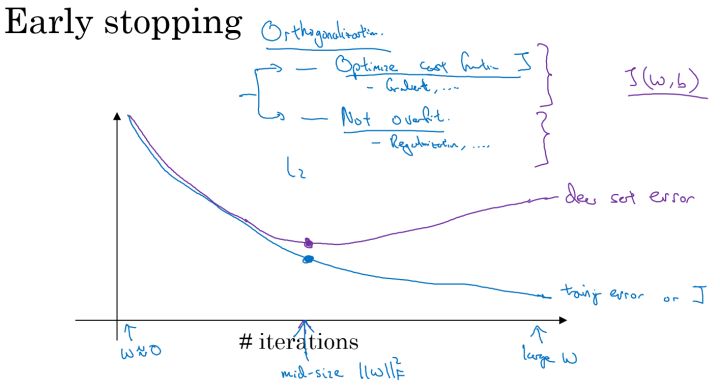
然而，Early Stopping有其自身的缺点，通常来说，机器学习训练模型有两个目标：一是优化cost function，尽量减小 $J$ ；二是防止过拟合。这两个目标彼此对立的，即减小 $J$ 的同时可能会造成过拟合，反之亦然。

但是，Early Stopping的做法通过减少得带训练次数来防止过拟合，这样J就不会足够小。也就是说，early Stopping将上述两个目标融合在一起，同时优化，但可能没有“分而治之”的效果好。

标准化(归一化)输入(Normalizing inputs)

使用标准化处理输入 $X$ 能够有效加速收敛。标准化输入就是对训练数据集进行归一化的操作，即将原始数据减去其均值 $\mu$ 后，再除以其方差 $\sigma^2$ ：

$x = \frac{x - \mu}{\sigma^2}$

其中：

$\mu = \frac{1}{m}\sum_{i=1}^{m}x^{(i)}$ $\sigma = \sqrt{\frac{1}{m}\sum_{i=1}^{m}x^{ {(i)}^2}}$

以二维平面为例，下图展示了其归一化过程：

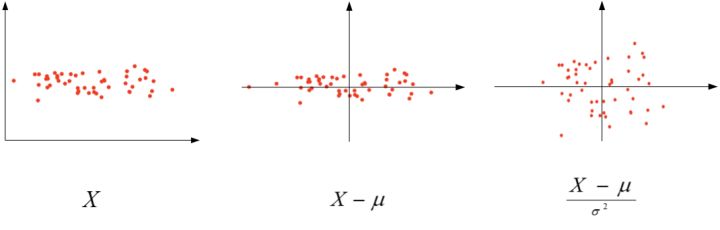
值得注意的是，由于训练集进行了标准化处理，那么对于测试集或在实际应用时，应该使用同样的 $\mu$ 和 $\sigma^2$ 对其进行标准化处理。这样保证了训练集合测试集的标准化操作一致。

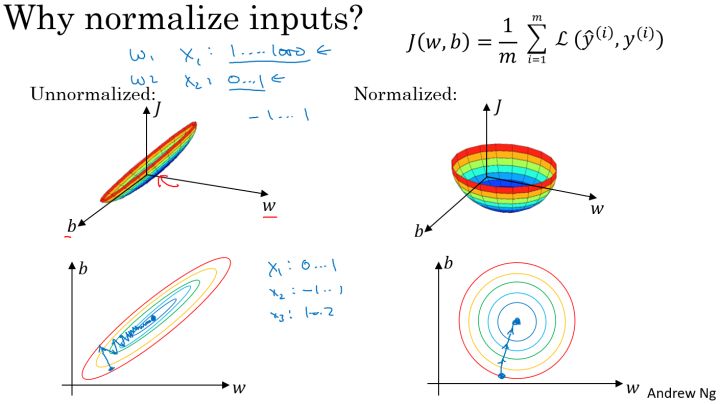
在不使用归一化的代价函数中，如果我们设置一个较小的学习率，那么很可能我们需要很多次迭代才能到达代价函数全局最优解；如果使用了归一化，那么无论从哪个位置开始迭代，我们都能以相对很少的迭代次数找到全局最优解。

梯度消失和梯度爆炸(Vanishing / Exploding gradients)

梯度消失和梯度爆炸。意思是当训练一个层数非常多的神经网络时，计算得到的梯度可能非常小或非常大，甚至是指数级别的减小或增大。这样会让训练过程变得非常困难。

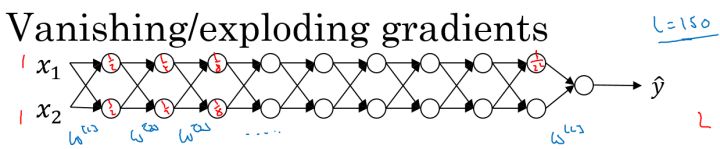
$W^{[l]}=\left[ \begin{array}{l}1.5 & 0 \\ 0 & 1.5\end{array} \right]$ 便于分析，我们令各层的激活函数为线性函数，忽略各层常数项b的影响，即假定 $g(Z) = Z, b^{[l]} = 0$，对于目标输出有：

$\hat{Y} = W^{[L]}W^{[L-1]}...W^{[2]}W^{[1]}X$

如果各层权重 $W^{[l]}$ 的元素都稍大于 1 ，例如 1.5, $W^{[l]}=\left[ \begin{array}{l}1.5 & 0 \\ 0 & 1.5\end{array} \right]$，则预测输出 $\hat{Y}$ 将正比于 $1.5^{L}$ 。$L$ 越大， $\hat{Y}$ 越大，且呈指数型增长。我们称之为数值爆炸。
相反，如果各层权重 $W^{[l]}$ 的元素都稍小于 1，例如 0.5，$W^{[l]}=\left[ \begin{array}{l}0.5 & 0 \\ 0 & 0.5\end{array} \right]$ ，则预测输出 $\hat{Y}$ 将正比于 $0.5^{L}$ 。网络层数L越多， $\hat{Y}$ 呈指数型减小。我们称之为数值消失。

神经网络的权重初始化(Weight Initialization for Deep NetworksVanishing /Exploding gradients)

利用初始化缓解梯度消失和爆炸问题.

根据

$z={w}_1{x}_1+{w}_2{x}_2 + ... + {w}_n{x}_n + b$

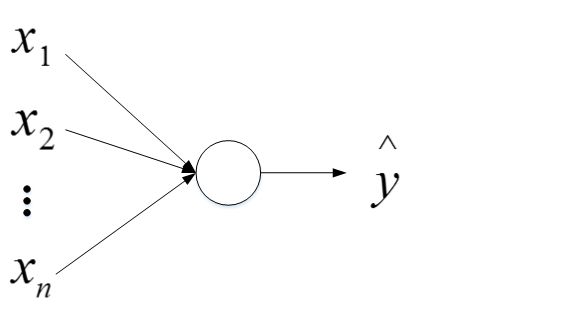
思路是让$w$与$n$有关，且$n$越大，$w$应该越小才好。这样能够保证$z$不会过大:

不同激活函数的参数初始化：

激活函数使用ReLu：令 $W$ 方差$Var(w_i) = \frac{2}{n}$，相应的python代码是：
```
  WL = np.random.randn(WL.shape[0], WL.shape[1]) * np.sqrt(1/n)
```
激活函数使用tenh：令 $W$ 方差$Var(w_i) = \frac{1}{n}$，相应的python代码是：
```
  w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(2/n[l-1])  
```
其中$n$是输入的神经元个数，也就是 $n^{[l-1]}$。

梯度的数值逼近(Numerical approximation of gradients)

在实施 backprop 时，有一个测试叫做梯度检验，其目的是检查验证反向传播过程中梯度下降算法是否正确。该小节将先介绍如何近似求出梯度值。

使用双边误差的方法去逼近导数，精度要高于单边误差。

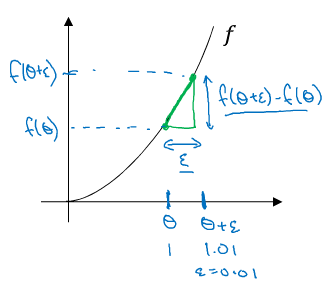
单边误差：$f’(\theta) = {\lim_{\varepsilon\to 0}} = \frac{f(\theta + \varepsilon) - (\theta)}{\varepsilon}$，误差：$O(\varepsilon)$

双边误差： $f’(\theta) = {\lim_{\varepsilon\to 0}} = \frac{f(\theta + \varepsilon) - (\theta - \varepsilon)}{2\varepsilon}$，误差：$O(\varepsilon^2)$

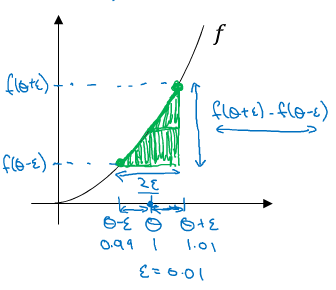
当 $ε$ 越小时，结果越接近真实的导数，也就是梯度值。可以使用这种方法来判断反向传播进行梯度下降时，是否出现了错误。

梯度检验(Gradient checking)

下面用前面一节的方法来进行梯度检验：

连接参数

将 $W^{[1]}$，$b^{[1]}$，…，$W^{[L]}$，$b^{[L]}$ 全部连接出来，成为一个巨型向量 $θ$。这样，

$J(W^{[1]}, b^{[1]}, ..., W^{[L]}，b^{[L]})=J(\theta)$

同时，对 $dW^{[1]}$，$db^{[1]}$，…，$dW^{[L]}$，$db^{[L]}$ 执行同样的操作得到巨型向量 $dθ$，它和 $θ$ 有同样的维度。

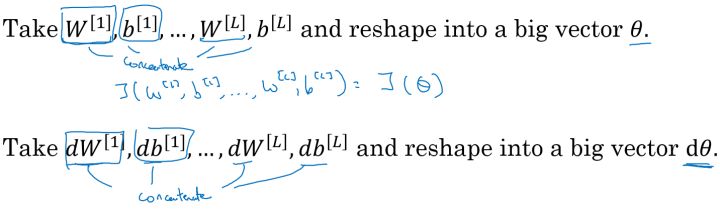
接着利用 $J(\theta)$ 对每个 $\theta_i$ 计算近似梯度，其值与反向传播算法得到的 $d\theta_i$ 相比较，检查是否一致。例如，对于第i个元素，近似梯度为：

$d\theta_{approx}[i] ＝ \frac{J(\theta_1, \theta_2, ..., \theta_i+\varepsilon, ...) - J(\theta_1, \theta_2, ..., \theta_i-\varepsilon, ...)}{2\varepsilon}$

应该

$\approx{d\theta_{[i]}} = \frac{\partial J}{\partial \theta_i}$

因此，我们用梯度检验值

$\frac{ {||d\theta_{approx} - d\theta||}_2}{ {||d\theta_{approx}||}_2+{||d\theta||}_2}$

检验反向传播的实施是否正确。其中，

${||x||}_2 = \sum^N_{i=1}{|x_i|}^2$

表示向量 $x$ 的 L2-范数（也称“欧几里德范数”），它是误差平方之和，然后求平方根，得到的欧氏距离。

如果梯度检验值和 $ε$ 的值相近，说明神经网络的实施是正确的，否则要去检查代码是否存在 bug。

一般来说，如果欧氏距离越小，例如 $10^{-7}$ ，甚至更小，则表明 $d\theta_{approx}$ 与 $d\theta$ 越接近，即反向梯度计算是正确的，没有bugs。
如果欧氏距离较大，例如 $10^{-5}$ ，则表明梯度计算可能出现问题，需要再次检查是否有bugs存在。
如果欧氏距离很大，例如 $10^{-3}$ ，甚至更大，则表明 $d\theta_{approx}$ 与 $d\theta$ 差别很大，梯度下降计算过程有bugs，需要仔细检查。

梯度验证应用的注意事项(Gradient Checking Implementation Notes)

不要在训练中使用梯度检验，它只用于调试(debug),因为时间代价比较大。
如果算法的梯度检验失败，要检查所有项，并试着找出 bug，即确定哪个 $dθapprox[i]$ 与 $dθ$ 的值相差比较大；
当成本函数包含正则项时，也需要带上正则项进行检验；
梯度检验不能与 dropout 同时使用。因为每次迭代过程中，dropout 会随机消除隐藏层单元的不同子集，难以计算 dropout 在梯度下降上的成本函数 $J$。建议关闭 dropout，用梯度检验进行双重检查，确定在没有 dropout 的情况下算法正确，然后打开 dropout；

本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：黄钢的博客，同时保持文章内容的完整和以上声明信息！

"deeplearning.ai-Class2-Week1"