前言
本篇博客是 Andrew NG 《Machine Learning Yearning》 的「第五章:学习曲线」翻译。本章内容将提供一个更加丰富和直观的方式,来帮助你更好地将偏差归因到可避免偏差或者是方差上。
👉官网传送门
👉GitHub 项目传送门,欢迎 Star
28. 诊断偏差和方差:学习曲线
我们已经见过一些方法,并使用它们来估计有多少误差被归因到可避免偏差或者是归因到方差上。比如,我们通过估计最优误差和计算学习算法的训练集和开发集误差做到了这一点。现在,让我们来讨论一个信息量更大的方法:绘制学习曲线(Learning Curves)。
学习曲线以你的训练样本的数量为横轴,误差为纵轴。要绘制它,你可以使用不同的训练集大小来重复运行算法,得出在不同训练集大小下的开发集误差。比如,你总共有 1000 个样本,则可以让算法分别在 100、200、300、……、1000 大小的样本尺寸下进行训练,然后绘制出在训练集大小不断增大下的开发集误差的变化趋势,如下图:
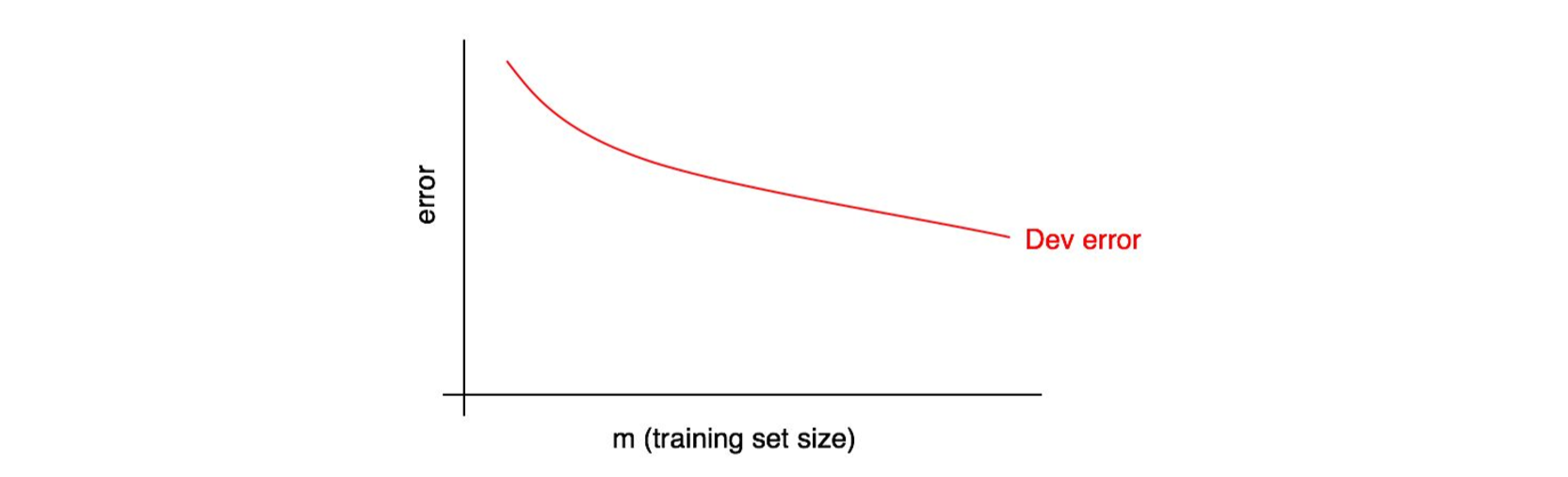
随着训练集大小的增加,开发集误差在下降。
「期望误差率(Desired Error Rate)」是我们希望学习算法能够最终达到的那个表现水平,例如:
- 如果我们希望达到「人类表现水平」,那么「期望误差率」指的就是人类误差率;
- 如果我们的学习算法为特定的产品提供服务(例如为猫 App 提供猫咪识别器),我们可能会需要一种直觉,来发觉需要达到怎么的表现水平的算法才能给用户提供一个绝佳的体验。
- 如果你长期从事在一个关键的应用程序上,那么你可能具备这个直觉,能够预计出在下季度/下一年中能够取得多大的进展。
所以,将期望的表现水平添加到你的学习曲线中:
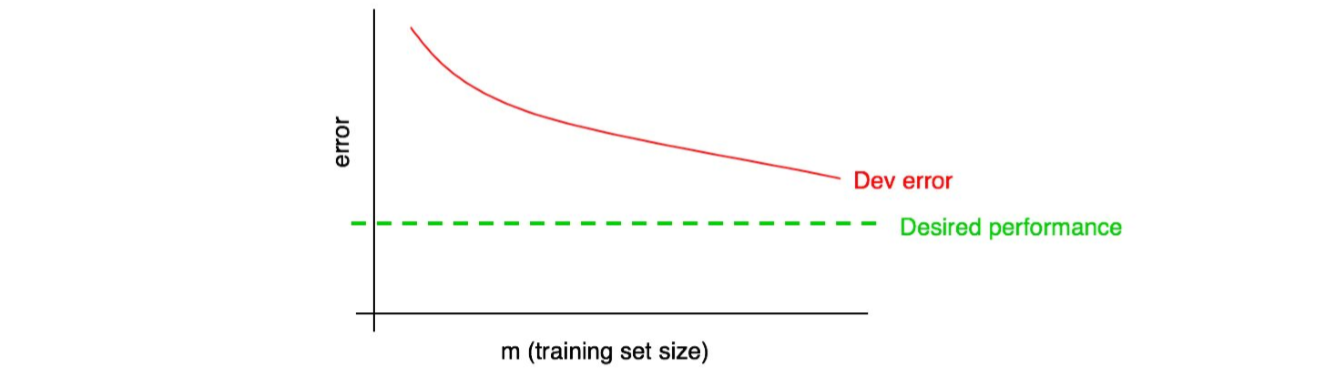
在图中,可以管观察红色的开发误差曲线,从而猜测出可以通过添加更多的数据来算法达到期望的性能水平。在上图展示的例子中,通过加倍训练集尺寸来促使学习算法朝着期望的性能改进看起来是合理的。
但是,假设开发误差曲线已经被「压平了(Plateaued)」,下图,你就能够立刻反应过来,继续添加数据已经不能够帮助你的算法往目标逼近了:
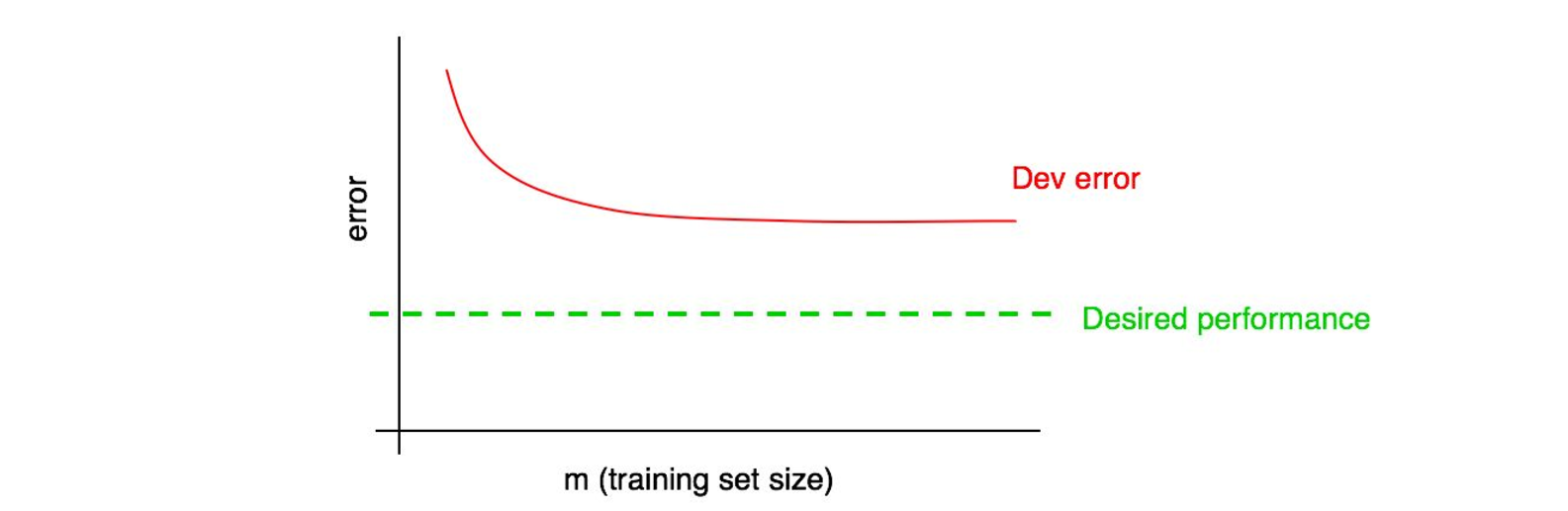
通过观察学习曲线,你可能就能避免在花费了数月时间收集多达两倍的训练数据后,才意识到这对优化性能并没有帮助。
这个过程的一个缺点是:如果你只关注开发误差曲线,在有大量数据的情况下你很难推断和预测红色曲线的走势。所以,现在有另外一根额外的曲线可帮助你评估添加更多数据对性能的影响:训练误差曲线。
29. 绘制训练误差曲线
随着训练集大小的增加,你的开发集(和测试集)的误差应该会减少;但是随着训练集大小的增加,你的训练集的误差应该是会增加的。
让我们以例子来说明这种情况,假设你的训练集只有两个样本:一个猫图和一个非猫图。然后学习算法很容易的就学习到了训练集中的这两个样本,并达到了 0% 的训练集误差。即使其中一个或者两个训练样本的标签都被标记错误了,对于学习算法来说,仍然能够轻松的记住这两个标签。
现在假设你的训练集有 100 个样本,也许有一些例子时被错误标记的,或者是模棱两可——图片模糊到即使是人类也无法分辨图片中有无猫。也许学习算法仍然能够「记忆」大部分或全部训练集样本,但也很难取得 100% 的准确率了。通过将训练集样本量从 2 个增加到 100 个,你会发现训练集准确率会稍微下降。
最后,假设你的训练集有 10000 个样本,在这种情况下,算法更加难以去拟合这 10000 个样本了,特别是还存在模糊图片或者时标记错误图片的情况下。因此你的算法表现在训练集上会变得更差。
让我们将训练误差曲线绘制到之前的那张图上:
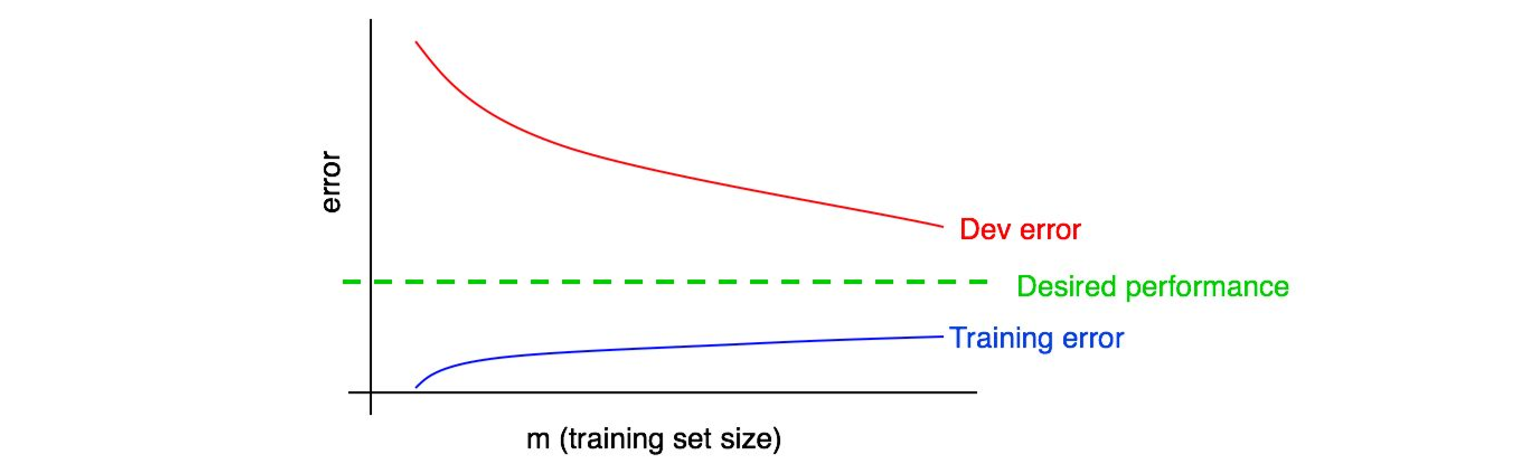
你可以看到蓝色的「训练误差曲线」是随着训练集样本量的增大而增大的。此外,你的算法的在训练集上的表现通常要好于开发集,因此,红色的开发及误差曲线一般来说会严格地高于训练误差曲线。
接下来,让我们讨论如何解读这些曲线图。
30. 解读学习曲线:高偏差
假设你的开发误差曲线看起来是这样的:
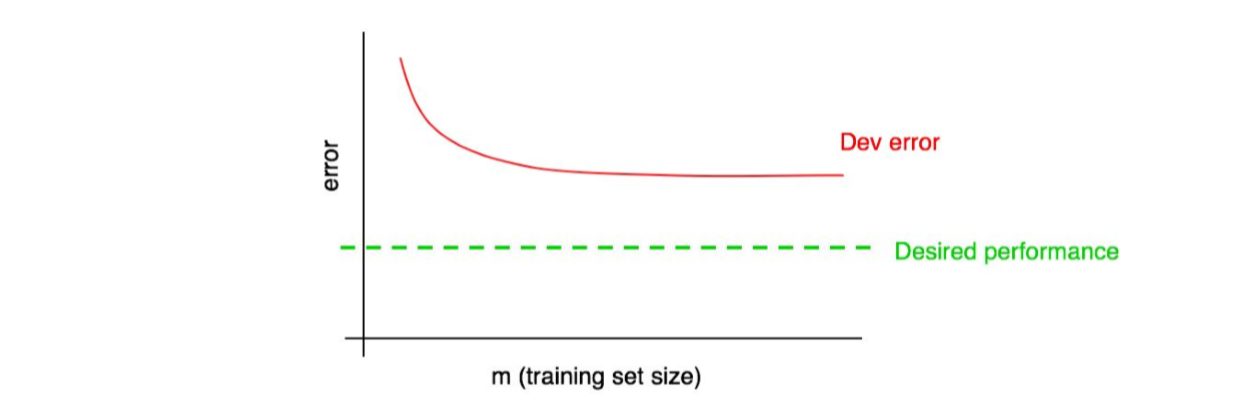
我们之前说过,如果你的开发误差曲线平稳,也就是说,无法通过添加数据来让算法达到期望的性能。
但是我们很难切确的知道红色的开发误差曲线的外推(外推法)是怎样的。如果开发集很小,则更不确定,因为曲线可能是有噪声的。
假设我们将训练误差曲线添加到该图中并得到以下结果:
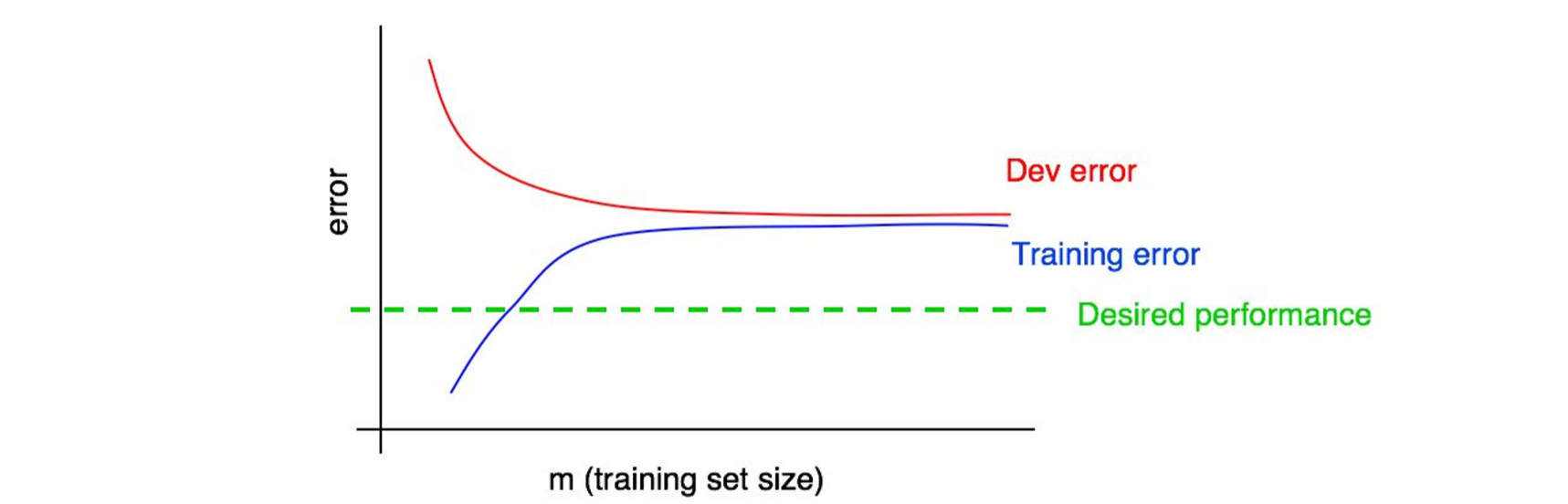
现在,你可以绝对确定,添加更多的数据本身是无效的。为什么?记住我们下面提到两个结论:
- 随着我们添加越来越多的训练数据,训练误差只会越来越大。因此,蓝色的训练误差曲线只能够保持当前水平或者更糟糕(曲线趋势往上),所以随着训练集数据的增多,曲线会往远离期望性能曲线(绿线)的方向发展。
- 红色的开发误差曲线通常高于蓝色训练误差曲线,意味着,当训练误差曲线都高于期望性能曲线(绿线)并有继续远离的趋势的时候,几乎不可能通过添加数据的方式来让红色的开发误差曲线下降到期望的性能水平。
在同一个图表上同时检查开发误差曲线和训练误差曲线。使我们能够更加自信的去推断开发误差曲线。
为了更好的阐述,假设我们把对最优误差的估计作为期望性能表现,那么上图就是一个教科书式的关于一个具有高可避免偏差的学习曲线的例子:在最大的训练集规模下(大概理解为对应于我们所有的训练数据),训练误差和期望误差之间存在很大的差距(进步空间),说明该案例遇到了高可避免偏差问题。此外,训练误差曲线和开发误差曲线的差距很小,意味着方差不大。
以前,我们只在该图的最右点来测量训练集和开发集的误差,这个点与我们算法使用了全部可用训练数据相对应。而绘制完整的学习曲线可以让我们更加全面的了解在不同训练集大小下的算法性能表现。
31. 解读学习曲线:其他情况
来看下面这个学习曲线图:
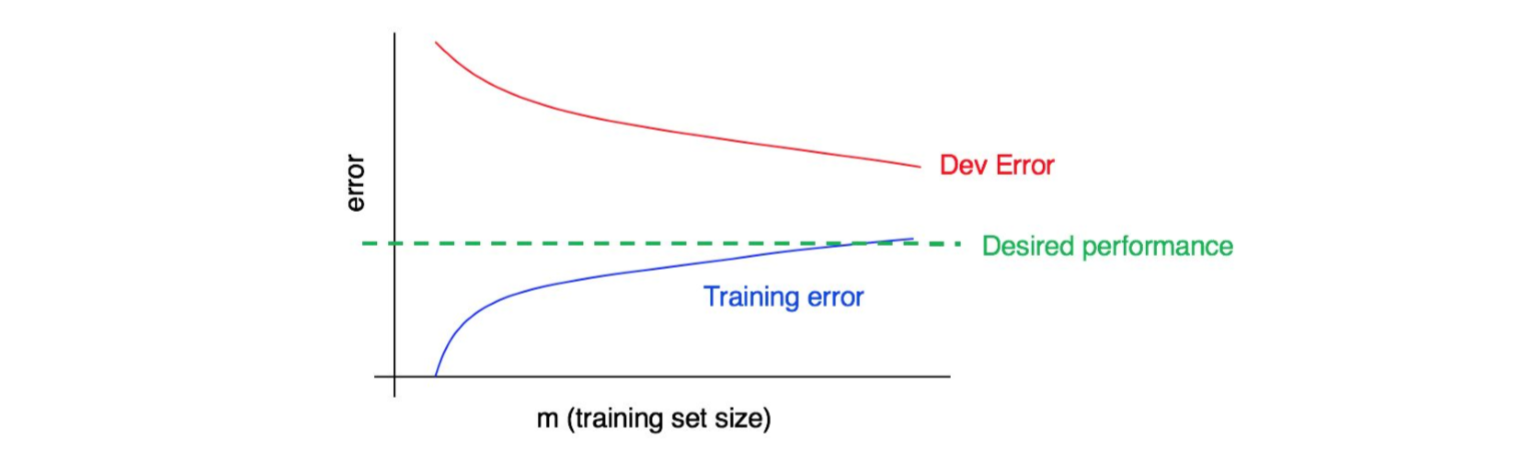
这张趋势图体现出了高方差、高偏差还是两者都有?
这条蓝色的训练误差曲线相对较低,然后红色的这条开发误差曲线则远高于蓝色的训练误差曲线。因此,该情况属于偏差很小方差很大情况。则,增加更多的训练数据可能有助于减小开发误差和训练误差之间的差距。
现在,曲线图变成这样:
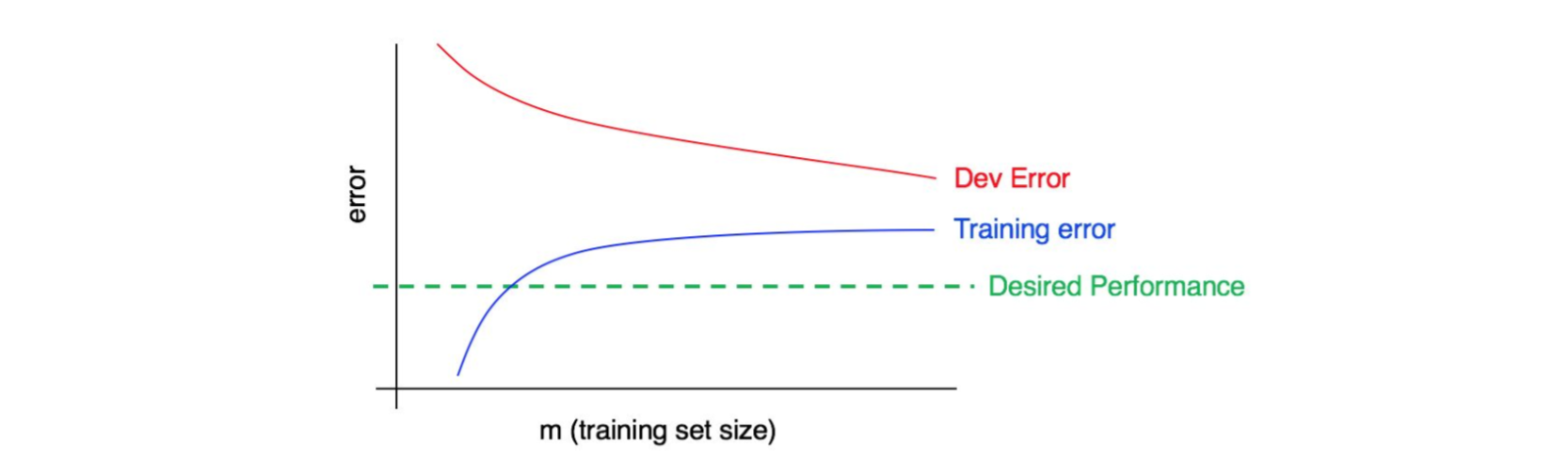
这一次,训练误差(蓝线)变得很大,因为它远高于期望的性能水平(绿线)。而开发误差(红线)也比训练误差大得多。因此,这种情况同时存在这高方差和高偏差问题。你必须找到一种方法来减少算法中的高偏差和高方差。
32. 绘制学习曲线
假设你有一个非常小的训练集(100 个样例)。你可以使用随机挑选的 10 个样本组成的子集,然后是 20 个样本组成的子集,然后是 30 个……一直到 100 个样本的集合来训练算法——以 10 的间隔递增。然后用这 10 个数据点来绘制学习曲线,你可能就会发现,在小的训练集下,曲线看起来波动很大(意思是这些值比预期值要高/或者低)。
当只对10个随机选择的样本进行训练时,脸黑的时候你可能会随机出了一个垃圾训练集——有很多模糊/标记错误的样本。或许,你很幸运的得到了一个很好的训练集。一个很小的训练集意味着开发误差和训练误差会很容易出现随机的波动。
如果你的机器学习应用严重偏好于某一类(比如在猫咪分类任务中,反例的分数比正例的要大的多),或者如果训练任务中需要识别大量的类(例如识别 100 种不同的动物种类),那么选择出那种特别「不具代表性」或者是坏的训练集的机会也更大。例如,如果你的总样本中有 80% 都是负例样本(y=0),而只有 20% 是正例样本(y=1),那么很有可能随机抽样出来的那 10 个样本组成的子集里边只包含了负例样本,这样的话算法很难学习出一些有意义的东西来。
如果训练曲线中因为噪声的原因使得我们很难观察到真实的变化趋势,这里提供两个解决方案:
- 放弃使用在10个样本的数据集上训练一个模型的方法,取而代之1的是从 100 个原始集合中随机抽样几个(3-10)由 10 个样本组成的数据子集作为训练集。然后在每个训练子集上训练出模型来,并计算出每个模型的训练误差和开发误差。最后计算并绘制它们的平均训练误差和平均开发误差。
- 如果你的训练集偏向某一类,或者是如果有很多类别,请选择一个「均衡」一点的子集,而不是简单的从 100 个样本中随机抽取 10 个。举例子来说,如果你切确知道你的样本中那个 20% 是正例样本,80% 是反例样本,合理的做法就是,你应该尽量保证每个类的样本所占的比例尽可能接近原始训练集的整体比例。
除非你已经尝试去画了学习曲线,并且认为画出来的线波动过大以至于没办法观察到本质的变化趋势,否则我不会去为这些技术烦恼。如果你的训练集很大——10000 个样本——并且你的类别分布比较均衡,那么上述的技术你可能用不上。
最后,绘制学习曲线的计算成本可能很高:例如,假设你可能需要训练 10 个模型出来——从 1000 个,然后是 2000 个……一直到 10000 个样本。因为使用小数据集训练要比使用大数据集训练快得多,所以,实际上并不是像上面那样均匀地将训练集大小按照线性步长来划分,更通用的是将训练集划分为 1000 个、2000 个、4000 个、6000 个和 10000 个样本的集合,然后训练它们得到对应的模型参数。这应该仍然能够让你清楚的了解学习曲线的趋势。当然,只有在训练模型的计算成本很大的时候,这种技术才有意义。
-
这里的采样和替换的意思是:你从 100 个样本中随机挑选 10 个样本组成第一个训练子集。然后为了组成第二套训练子集,重新挑选 10 个样本(依旧从 100 个样本中挑)。因此,一个例子可能同时出现在第一和第二套训练子集里边。相比之下,如果你没有使用替换去采样,第二套训练子集则从第一套抽样完之后剩余的 90 个中挑选。当然,在实际操作中,两种方法并不会有太多差异,但前者是常见的做法。 ↩
本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。欢迎转载,并请注明来自:黄钢的博客 ,同时保持文章内容的完整和以上声明信息!