GitHub项目传送门
欢迎Star
本篇博客有大量公式演示,不推荐使用手机查看
深层神经网络的前向传播和反向传播(Forward and backward propagation)
前向传播
以上面讲过的4层神经网络为例
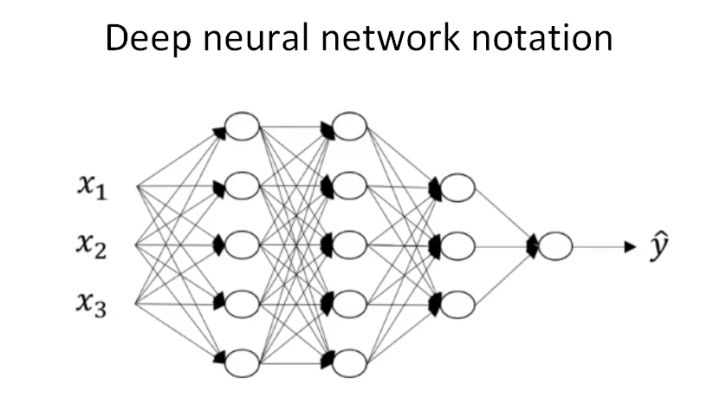
输入 :$a^{[l-1]}$
输出 :$a^{[l]}$,cache($z^{[l]}$)
公式 :
反向传播
输入 :$da^{[l]}$
输出 :$da^{[l-1]}$,$dW^{[l]}$,$db^{[l]}$
公式 :
如果有$m$个训练样本,对于第 $l$ 层,其正向传播过程的 $Z^{[l]}$ 和 $A^{[l]}$ 可以表示为:
核对矩阵的维数(Getting your matrix dimensions right)
对于单个训练样本,输入$x$的维度是$(n^{[0]},1)$神经网络的参数 $W^{[l]}$ 和 $b^{[l]}$ 的维度分别是:
其中, $l=1,\cdots,L$ , $n^{[l]}$ 和 $n^{[l-1]}$ 分别表示第 $l$ 层和 $l-1$ 层的所含单元个数。 $n^{[0]}=n_x$ ,表示输入层特征数目。
反向传播过程中的 $dW^{[l]}$ 和 $db^{[l]}$ 的维度分别是:
注意到, $W^{[l]}$ 与 $dW^{[l]}$ 维度相同, $b^{[l]}$ 与 $db^{[l]}$ 维度相同。
对于 $z$、$a$,向量化之前有:
$z^{[l]}$ 和 $a^{[l]}$ 的维度是一样的,且 $dz^{[l]}$ 和 $da^{[l]}$ 的维度均与 $z^{[l]}$ 和 $a^{[l]}$ 的维度一致。
而在$m$个样本的向量化之后,输入矩阵X的维度是$(n^{[0]},m)$,需要注意的是 $W^{[l]}$ 和 $b^{[l]}$ 的维度与只有单个样本是一致的:
是因为在运算 $Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$ 中, $b^{[l]}$ 会被当成$(n^{[l]},m)$矩阵进行运算,这是因为python的广播性质,且 $b^{[l]}$ 每一列向量都是一样的。 $dW^{[l]}$ 和 $db^{[l]}$ 的维度分别与$ W^{[l]} $和$ b^{[l]}$ 的相同。
但是, $Z^{[l]}$ 和 $A^{[l]}$ 的维度发生了变化:
在计算反向传播时,$dZ$、$dA$ 的维度和 $Z$、$A$ 是一样的。
使用深层网络的原因(Why deep representations?)
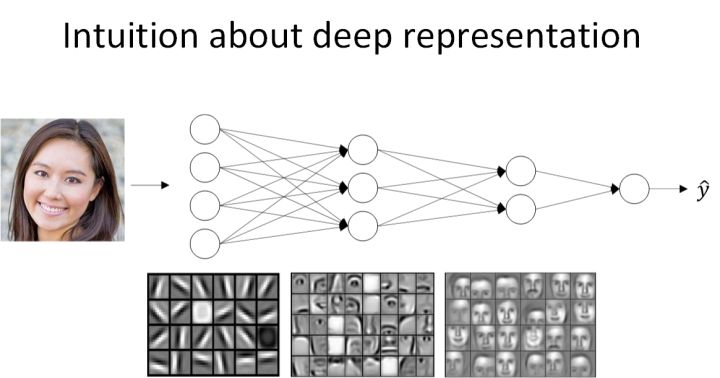
- 经过训练,神经网络第一层所做的事就是从原始图片中提取出人脸的轮廓与边缘,即边缘检测。这样每个神经元得到的是一些边缘信息。
- 神经网络第二层所做的事情就是将前一层的边缘进行组合,组合成人脸一些局部特征,比如眼睛、鼻子、嘴巴等。
- 再往后面,就将这些局部特征组合起来,融合成人脸的模样。
可以看出,随着层数由浅到深,神经网络提取的特征也是从边缘到局部特征到整体,由简单到复杂。可见,如果隐藏层足够多,那么能够提取的特征就越丰富、越复杂,模型的准确率就会越高。
神经网络从左到右,神经元提取的特征从简单到复杂。特征复杂度与神经网络层数成正相关。特征越来越复杂,功能也越来越强大。
参数和超参数(Parameters vs Hyperparameters)
参数 即是我们在过程中想要模型学习到的信息(模型自己能计算出来的),例如 $W^{[l]}$,$b^{[l]}$。而 超参数(hyper parameters) 即为控制参数的输出值的一些网络信息(需要人经验判断)。超参数的改变会导致最终得到的参数 $W^{[l]}$,$b^{[l]}$ 的改变。
典型的超参数有:
- 学习速率:α
- 迭代次数:N
- 隐藏层的层数:L
- 每一层的神经元个数:$n^{[1]}$,$n^{[2]}$,…
- 激活函数 g(z) 的选择
本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。欢迎转载,并请注明来自:黄钢的博客 ,同时保持文章内容的完整和以上声明信息!