GitHub项目传送门
欢迎Star
本篇博客有大量公式演示,不推荐使用手机查看
神经网络表示(Neural Network Representation)
竖向堆叠起来的输入特征被称作神经网络的 输入层(the input layer)。
神经网络的 隐藏层(a hidden layer) 。“隐藏”的含义是 在训练集中,这些中间节点的真正数值是无法看到的。
输出层(the output layer) 负责输出预测值。
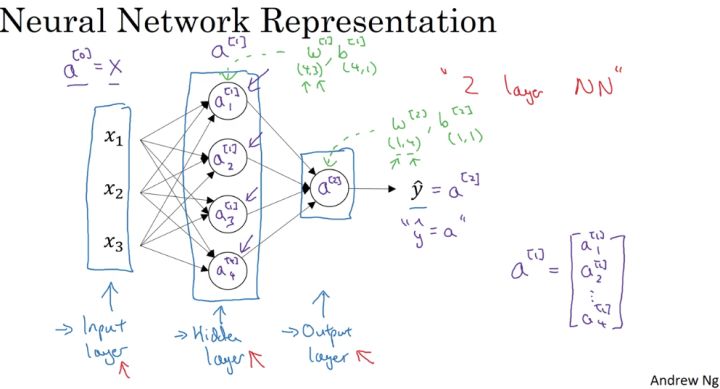
神经网络基本的结构和符号可以从上面的图中看出,这里不再复述。
主要需要注意的一点,是层与层之间参数矩阵的规格大小:
输入层和隐藏层之间
- $w^{[1]}->(4,3)$ :前面的 4 是隐层神经元的个数,后面的 3 是输入层神经元的个数;
- $b^{[1]}->(4,1)$ :和隐藏层的神经元个数相同; 隐藏层和输出层之间
- $w^{[1]}->(1,4)$ :前面的 1 是输出层神经元的个数,后面的 4 是隐层神经元的个数;
- $b^{[1]}->(1,1)$ :和输出层的神经元个数相同;
由上面我们可以总结出,在神经网络中,我们以相邻两层为观测对象,前面一层作为输入,后面一层作为输出,两层之间的$w$参数矩阵大小为 $(n_{out},n_{in})$ ,$b$参数矩阵大小为 $(n_{out},1)$ ,这里是作为 $z = wX+b$ 的线性关系来说明的,在神经网络中, $w^{[i]}=w^{T}$ 。
在logistic regression中,一般我们都会用 $(n_{in},n_{out})$ 来表示参数大小,计算使用的公式为:$ z = w^{T}X+b$ ,要注意这两者的区别。
神经网络输出(Computing a Neural Network’s output)
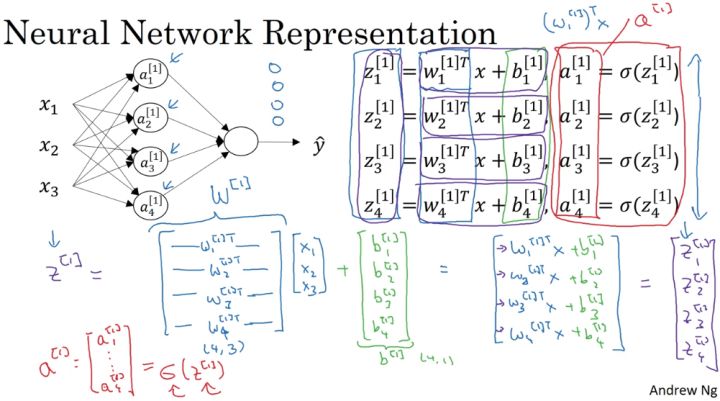
除输入层之外每层的计算输出可由下图总结出:
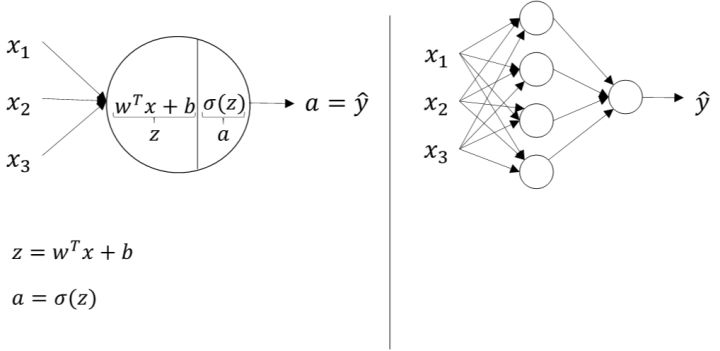
如下图所示,逻辑回归的正向计算可以分解成计算z和a的两部分:
对于两层神经网络,从输入层到隐藏层对应一次逻辑回归运算;从隐藏层到输出层对应一次逻辑回归运算。每层计算时,要注意对应的上标和下标,一般我们记上标方括号表示layer,下标表示第几个神经元。例如 $a_i^{[l]}$表示第$l$层的第$i$个神经元。注意,$i$从1开始,$l$从0开始。
下面,我们将从输入层到输出层的计算公式列出来:
然后,从隐藏层到输出层的计算公式为:
其中 $a^{[1]}$为列向量:
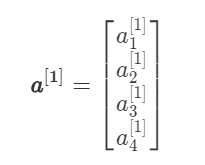
上述每个节点的计算都对应着一次逻辑运算的过程,分别由计算$z$和$a$两部分组成。
为了提高程序运算速度,我们引入向量化和矩阵运算的思想,将上述表达式转换成矩阵运算的形式:
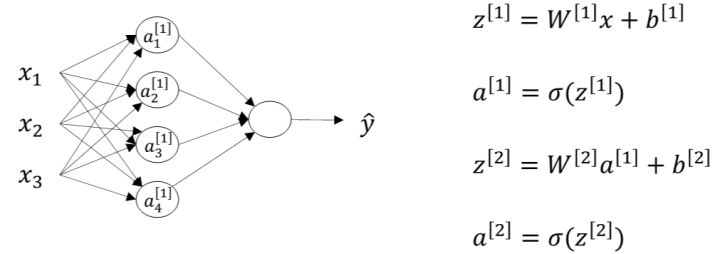
之前也介绍过,这里顺便提一下, $W^{[1]}$的维度是$(4,3)$, $b^{[1]}$的维度是$(4,1)$,$ W^{[2]}$的维度是$(1,4)$, $b^{[2]}$的维度是$(1,1)$。这点需要特别注意。
多样本的向量化(Vectorizing across multiple examples)
上一部分我们只是介绍了单个样本的神经网络正向传播矩阵运算过程。而对于$m$个训练样本,我们也可以使用矩阵相乘的形式来提高计算效率。而且它的形式与上一部分单个样本的矩阵运算十分相似,比较简单。
之前我们也介绍过,在书写标记上用上标$(i)$表示第$i$个样本,例如 $x^{(i)}$, $z^{(i)}$, $a^{2}$。对于每个样本$i$,可以使用for循环来求解其正向输出:
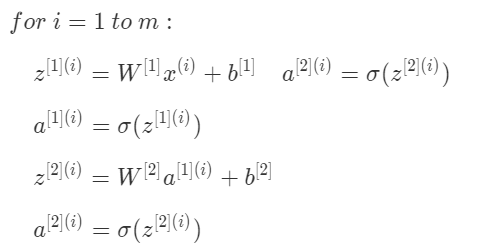
不使用for循环,利用矩阵运算的思想,输入矩阵X的维度为$(n_x,m)$。这样,我们可以把上面的for循环写成矩阵运算的形式:
$Z^{[1]}=W^{[1]}X+b^{[1]} $
$A^{[1]}=\sigma(Z^{[1]}) $
$Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]} $
$A^{[2]}=\sigma(Z^{[2]})$
其中, $Z^{[1]}$ 的维度是$(4,m)$,4是隐藏层神经元的个数; $A^{[1]}$的维度与 $Z^{[1]}$相同;$ Z^{[2]}$和 $A^{[2]}$的维度均为$(1,m)$。对上面这四个矩阵来说,均可以这样来理解:行表示神经元个数,列表示样本数目$m$。
激活函数(Activation functions)
有一个问题是神经网络的隐藏层和输出单元用什么激活函数。之前我们都是选用 sigmoid 函数,但有时其他函数的效果会好得多。
可供选用的激活函数有:
- tanh 函数(the hyperbolic tangent function,双曲正切函数):
效果几乎总比 sigmoid 函数好(除开 二元分类的输出层 ,因为我们希望输出的结果介于 0 到 1 之间),因为函数输出介于 -1 和 1 之间,激活函数的平均值就更接近 0,有类似数据中心化的效果。
然而,tanh 函数存在和 sigmoid 函数一样的缺点:当 $z$ 趋紧无穷大(或无穷小),导数的梯度(即函数的斜率)就趋紧于 0,这使得梯度算法的速度大大减缓。
- ReLU 函数(the rectified linear unit,修正线性单元) :
当 $z > 0$ 时,梯度始终为 1,从而提高神经网络基于梯度算法的运算速度,收敛速度远大于 sigmoid 和 tanh。然而当 $z < 0$ 时,梯度一直为 0,但是实际的运用中,该缺陷的影响不是很大。
- Leaky ReLU(带泄漏的 ReLU):
Leaky ReLU 保证在 $z < 0$ 的时候,梯度仍然不为 0。理论上来说,Leaky ReLU 有 ReLU 的所有优点,但在实际操作中没有证明总是好于 ReLU,因此不常用。
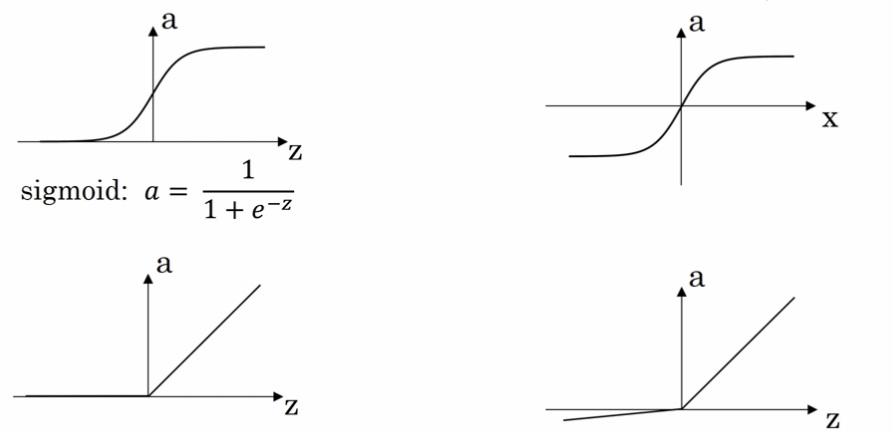
在选择激活函数的时候,如果在不知道该选什么的时候就选择 ReLU,当然也没有固定答案,要依据实际问题在交叉验证集合中进行验证分析。当然,我们可以在不同层选用不同的激活函数。
使用非线性激活函数的原因:
使用线性激活函数和不使用激活函数、直接使用 Logistic 回归没有区别,那么无论神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当,就成了最原始的感知器了。
激活函数的导数(Derivatives of activation functions)
- sigmoid 函数:
- tanh 函数:
神经网络的梯度下降法(Gradient descent for neural networks)
正向梯度传播
仍然是浅层神经网络,包含的参数为 $W^{[1]}$, $b^{[1]}$, $W^{[2]}$, $b^{[2]}$。令输入层的特征向量个数 $n_x=n^{[0]}$,隐藏层神经元个数为 $n^{[1]}$,输出层神经元个数为 $n^{[2]}=1$。则 $W^{[1]}$的维度为$( n^{[1]}, n^{[0]})$, $b^{[1]}$的维度为$(n^{[1]},1)$, $W^{[2]}$的维度为$(n^{[2]}, n^{[1]})$, $b^{[2]}$的维度为$(n^{[2]},1)$。
该神经网络正向传播过程为 :
反向梯度下降
神经网络反向梯度下降公式(左)和其代码向量化(右):

随机初始化(Random+Initialization)
如果在初始时将两个隐藏神经元的参数设置为相同的大小,那么两个隐藏神经元对输出单元的影响也是相同的,通过反向梯度下降去进行计算的时候,会得到同样的梯度大小,所以在经过多次迭代后,两个隐藏层单位仍然是对称的。无论设置多少个隐藏单元,其最终的影响都是相同的,那么多个隐藏神经元就没有了意义。
在初始化的时候,$W$ 参数要进行随机初始化,不可以设置为 0。而$ b $因为不存在对称性的问题,可以设置为 0。
以 2 个输入,2 个隐藏神经元为例:
W = np.random.rand(2,2)* 0.01
b = np.zero((2,1))
这里将 $W$ 的值乘以 0.01(或者其他的常数值)的原因是为了使得权重 $W$ 初始化为较小的值,这是因为使用 sigmoid 函数或者 tanh 函数作为激活函数时,$W$ 比较小,则 $Z=WX+b$ 所得的值趋近于 0,梯度较大,能够提高算法的更新速度。而如果 $W$ 设置的太大的话,得到的梯度较小,训练过程因此会变得很慢。
ReLU 和 Leaky ReLU 作为激活函数时不存在这种问题,因为在大于 0 的时候,梯度均为 1。
本作品采用知识共享署名-相同方式共享 4.0 国际许可协议进行许可。欢迎转载,并请注明来自:黄钢的博客 ,同时保持文章内容的完整和以上声明信息!